まず、何度か書いているが、ここでも最初に書いておく。
ぶっちゃけると、「順列になってるリストを返す関数」「組み合わせになってるリストを返す関数」を書く、ってのは基本的には難問中の難問だ。
個人的な経験で言うと、SICPで紹介されてた「両替」の問題と合わせると、これらは再帰による三大難問と言って良く、ハッキリ言えばこれら以上の難問は見たことがない。
要するに、この世にはたくさん「再帰として書ける」プログラムはあるが、経験上、この「三大難問」以上に難しい再帰はねぇし、またこのレベルでの「再帰」の問題は他には存在せん、っちゅーこっちゃ。知ってる限りで言うと。
そういう意味では、これらは、あくまで「教養として」押さえておけば良い話であって、あるいは、「暗記だけ」しとけば良い、って話になる。
そして突出した難問だ、と言う事は、これらを利用するケースはあったとしても、応用するケースは「まずない」と言う事だ。
何故かと言うと、「思いもつかないようなプログラム」は所詮「思いもつかない」からである(笑)。
プログラミングも基本「再現性がある」から出来るわけだ。その「再現性がある知識」を応用するからこそ「あれをやってみよう」って思えるわけだよな。
だから、勉強する際には「再現性がある知識」をより広げる事が重要なんだけど。言い換えると「知識がある範疇の事柄」以外は思いつかない、ってのが人間の限界なわけだな。
ところが、「三大難問」くらいのレベルになると、応用の幅が極めて狭くなる。組み合わせは所詮組み合わせであり、順列も所詮順列だ。これらの仕組みを「応用」する、って事は出来ない。仮に「出来る」と言う人が現れた場合、そいつはプログラマと言うよか数学者だろう。数学者が作った数学は、残念ながら「数学のトーシロ」が簡単に、言っちゃえば「応用した定理」なんつーのは発見出来ない。そう、これはそういうレベルの話なんだ。
一旦証明された「順列」や「組み合わせ」そのものを使う事は出来るだろう。でもこれらを適用した「別の定理」なんざ、いくらプログラミングを極めても発見出来るような事はないから安心していい。もし発見出来たらそいつはフィールズ賞を受賞出来る可能性がある、ってこった(笑)。
従って、このレベルの再帰は「思いつこうとして思い付けるモノではない」って事になる。
もう1つ確認しておこう。再帰を書けるようになってくると「再帰が如何に簡単なのか」良く分かると思う。
ところが世の中には依然と「再帰は難しい」と言う誤解がある。それは実はこの「再帰三大難問」が関わってるから、なんだよ。
しかし本当に再帰って難しいのだろうか。もう一回ここで考えてみて欲しい。
仮に「再帰は難しい」と言うテーゼを認めたとしてみよう。じゃあ、これら「両替」、「順列」、「組み合わせ」の3つをforやwhileだと簡単に書けるのだろうか。暇な人は試してみて欲しい。恐らく「匙を投げる」結果になるとは思う。
つまり、「両替」「順列」「組み合わせ」は「反復構文」では書く事さえままならないんだが、辛うじて書ける、ってレベルへと再帰は「落としてくれてる」と言う事だ。これは再帰の仕組みが「簡単だから」成せる業なんであって、再帰が「難しかったら」そもそも書けない、って事を現していないか。
繰り返そう。実は再帰は「簡単」なんだ。
つまりだな。アルゴリズムの授業なんかでこれら3つを扱う場合、ここで初めて「反復構文じゃ解けない」ので、再帰が導入されるわけなんだけど。
そしてそれらの難問を再帰では解ける、って事を学ぶわけなんだけど、この時の「問題の難しさ」と言うのと「再帰で解いた」って印象が不幸にも強く結びつくんだな。
だから「再帰は難しい」と言う印象になるんだけど、事実は全然違う。
つまり「問題自体が難しい」と言うのと「プログラムを書く際での再帰と言うテクニックの難易度」ってのは実は全く関係がない。そう、単に「これらの問題が難しいだけ」なんだ。
これは考えてみれば当然だろう。ある捌くのが難しい魚があったとして、それを包丁で捌くとする。何とかその魚を捌いたとして、それは「その魚を捌くのが難しい」だけであって「包丁を使う事が難しい」わけじゃないだろう。
あるいは、ある数学の問題をコンピュータで解くのに試行錯誤したとする。それはその問題が難しいだけであって、必ずしも「コンピュータを使うのは難しい」にはならんだろ。
そういう事だ。
人間ってのはある印象を強く受けると、因果関係や相関関係を無視してその印象だけで発言する事がある。言っちゃえば理系はなるたけそういう発想はしないようにするもんなんだが、文系は良くそういう発想をする。そしてここで分かると思うけど、実はプログラマは理系発想ではない。こういう因果関係や相関関係を間違えてる事をヘーキで良く言うんだわ。
そして、「普段使い慣れてない」再帰を「難しい問題にだけ」適用して、要するに「不慣れなテクニックで」難易度の高い問題を解いた経験しかなければ「そりゃ嫌だ」って思う筈だろ(笑)。言わば当然の話となる。
逆に、普段から再帰慣れしてるけど、「それでも難しい問題がある」場合、それは単に「その問題が難しいだけなんだ」って思うだろう。別に「再帰が使いこなせてない」わけじゃあないんだ。難しい問題は単に難しい。それだけの話になる。
従って、「この問題が解けなくても」再帰が書ける、とか書けない、とかとは丸っきり関係がない、と言う事を押さえておこう。ある特定の魚を捌けなくても「包丁が使える/使えない」と言うのとは関係がない、ってのと同じだ。あるいは特定の数学の難問が解けない、と言うのと「コンピュータを使える/使えない」と言うのとは全く関係がない、ってのと同じだ。
大体、特定の数学の難問が解けなくてもコンピュータでエロ動画を観る事は可能だろ(笑)?エロ動画を観れる以上「コンピュータ自体を使う事が出来る」と言う事実は揺るがないわけだ(笑)。
とこれらの事を強く再確認してから、「組み合わせ」と言う話に入っていく。
まずはアルゴリズムの話をほっといて、次の例を見てみる。
例えば以前、順列を扱ったが、A, B, C, Dと言う組から2つ選ぶ順列は以下のようになる、って事は分かるだろう。
(A, B) (A, C) (A, D) (B, A) (B, C) (B, D) (C, A) (C, B) (C, D) (D, A) (D, B) (D, C)
一方、「組み合わせ」では次の6つが解となる。
{A, B} {A, C} {A, D} {B, C} {B, D} {C, D}
この2つの計算結果は何が違うんだろうか?
平たく言うと、順列はその定義によって「要素が置かれる順序」が重要となる。
しかし組み合わせはそうじゃない。大まかに言うと「要素が置かれる順序は関係がない」と言う事だ。
従って、順列では例えば
(A, B) ≠ (B, A)
だが、組み合わせでは
{A, B} = {B, A}
だ。
それが理由で一般に、組み合わせの「個数」は順列の「個数」より少なくなる。
さて、僕らはフツー、リストを使いまくってるわけだが。当然リストの要素間には「順序」がある。
この「順序がある」リストをあたかも「順序がない」ようにして扱おう、と言うのが問題を難しくしてるんだ。
ここで集合、と言う概念を紹介しておく。集合は簡単に言うと、何かの「集まり」ではあるが、原則「重複がなく」そして「順序がない」。
Lispの伝統芸としてはリストを集合としても使う、って事があるが、生憎その方針は完璧ではない。先程書いた通り、リスト内の要素は当然「同じ要素を違う位置に持っていても」良いし、そして「順序が大事」だからだ。
んで、実の事を言うと、Racketには集合を表すsetと言うデータ型がある。
> (equal? (set 1 2) (set 2 1))
#t
> (set 1 1)
(set 1)
>
見た通り、setはリストと違って順序がない。しかも重複を許さない。
そして組み合わせ、と言う「計算」は、リストじゃなくって、本質的には「集合に対する計算である」と言う事だ。
順列の項で、次のような関数permを作った。
(define (perm xs r)
(if (zero? r)
'(())
(append-map (lambda (x)
(map (lambda (ys)
(cons x ys)) (perm (remove x xs) (- r 1))))
xs)))
これも難問だったが、一応「理解不可能」と言うレベルではなかっただろう。
そして順列である以上、リストは解として「正しい」データ型だ。何故なら繰り返すが、リストは「重複を許し」、かつ「要素の位置情報」が重要なデータ型だからだ。
A、B、C、Dのグループから2つ選ぶ順列を生成させてみよう。
> (perm '(A B C D) 2)
'((A B) (A C) (A D) (B A) (B C) (B D) (C A) (C B) (C D) (D A) (D B) (D C))
>
そしてオチを言うと、「この解を全部集合に直して集合演算すれば」組み合わせに変換出来る、と言う事になる。
リストから集合への変換にはlist->setを用いる。
> (list->set (map list->set (perm '(A B C D) 2)))
(set (set 'B 'D) (set 'C 'B) (set 'A 'D) (set 'C 'A) (set 'B 'A) (set 'C 'D))
>
見事6つに減っている。集合が判断してる「重複」を全て取り除いてるから、だ。
結果のsetを見るのが嫌なら、若干データ変換が煩わしいが、またリストに直せば良い。
> (map set->list (set->list (list->set (map list->set (perm '(A B C D) 2)))))
'((D C) (A B) (A C) (D A) (B C) (D B))
>
結果のリストの順序がグチャグチャに見えるが、これでいいのである。と言うのも再度書くが、集合では順序は関係ない、からだ。その性質の為、リストに変換される際に整列なんぞしない。
いずれにせよ、直球勝負としては、順列リストを返す関数permを使って組み合わせのリストを返す関数を書く事が可能だ、と言う事だ。
(define (combinations xs r)
(map set->list (set->list (list->set (map list->set (perm xs r))))))
これならアルゴリズムもクソもない。単にデータ変換を行ってるだけ、で一応組み合わせのリストを生成出来る。効率さえ無視すればな(笑)。
ただ、うんうん悩んでドツボにハマるよりはよっぽど頭の良いやり方じゃないか、と思う。繰り返すが本質的なトコでは、「順序や重複を許す」リストと言うデータ型の利用が問題を難しくしてる、って事なんだ。逆に言うと適したデータ型を用いれば問題は比較的簡単になる、と言う証明でもある。「適したデータ型を選ぶ」と言うのは、言っちゃえば当たり前の話で、プログラミングの基本でもあるだろう。
ここでちと数学に入ろう。
とは言ってもシチメンド臭い話は避けよう。パスカルの三角形を利用する。

パスカルの三角形の要素は、頂点と辺を除けばその要素の上にあたる2つの要素の和、と言う事だった。
ところで、実はパスカルの三角形の全要素は「組み合わせ」の記号でも記述出来る。
つまりこういう事だ。

例えば4から2取る組み合わせの場合、
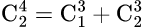
が成り立ってる、と言う事だ。
これが再帰を書く際のヒントとなる。
つまり、心臓部としては

が使えそうだ、と言う事だ。
実際これをそのまま再帰として使えるか否かはさておき、ちと実値がどうなってるのか、と言うのを調べてみよう。
パスカルの三角形の各要素がどういう集合を含んでるのか、と言うのは次のようになっている。

ここで例えば4から2つ取る組み合わせを見てみよう。
上のパスカルの三角形の表から見ると
{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}
なのは間違いないが、先程挙げた
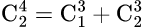
を適用してみようとしても当然成り立たないのだ(※1)。
{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}} ≠ {{1}, {2}, {3}} ∪ {{1, 2}, {1, 3}, {2, 3}}
そして「3から2つ選ぶ組み合わせ」は「4から2つ選ぶ組み合わせ」と要素数は一致するが、「3から1つ選ぶ組み合わせ」はそのままでは使えない。当然、要素数が足りないから、だ。
しかしながら「3から1つ選ぶ組み合わせ」の各集合に4と言う要素を加えれば帳尻が合う、と言う事に気づくのではないか。
{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}} = {{1, 4}, {2, 4}, {3, 4}} ∪ {{1, 2}, {1, 3}, {2, 3}}
これは上手く行きそうだ。これでプログラム上の再帰への取っ掛かりが出来る。
そしてベースケースだが、上のパスカルの三角形を見ると r = 0 の時、空の集合1つの集合になり、また r が引数として与えられた集合の大きさと同じだった場合、与えられた集合を含む集合にすれば良い、と言う事が分かる。
これらを鑑みると、再帰関数combinationは次のように書けば良い、と言う事が分かる筈だ。
見慣れない関数が出てると思うが、再帰の枠組みとしては何となく「簡単なんじゃ?」って思わないか。
この関数がやってる事は、先程書いた通りだ。
繰り返そう。
- 引数rが0の時、空集合の集合が返される(しかし含まれる集合の数が1にはなる、と言う事に気を付けよう)。
- 引数rが与えられた集合のサイズと同じ場合、その集合の集合を返す。 => {A, B, C, D}から4つ選べ、と言われたら {{A, B, C, D}} が解、にしか成りようがない。そしてそこに含まれている集合の個数はやっぱり1だ。
- それ以外の場合、今計算してるパスカルの三角形の上の段の、r - 1 番目と r 番目を調べて、前者には今の段で新しく得られた数をマッピングしながら追加し、両者の和集合を取る。
これだけ、だ。実は凄い簡単な事をやってる。ただし、今まで使った事のない関数を使ってるだけ、だ。
- set -> 集合を作成する。リストの場合のlistに相当する。
- set-count -> 集合の要素数を数える。リストの場合のlengthに相当する。
- set-rest -> 集合から1つ要素を取り除いた集合を返す。リストの場合のcdrに相当する。
- set-union -> 和集合を作る。リストの場合のappendに相当する。
- for/set -> Pythonでの集合内包表記に相当する。set-mapと言う高階関数も存在するが、返り値がリストになるので、今回は使用を見送ってる。
- set-add -> 集合に要素1つを追加する。リストの場合のconsに相当する。
- set-first -> 集合から1つ要素を取り出す。リストの場合のcarに相当する。
今まで使った事がない関数、と言えども、内情を説明されてしまえば「あ、リストでの再帰だと良く使う関数の代替だ」と気づくだろう。
そう、集合を使えば「組み合わせ」を書くのは特に難しくはないんだ。問題は、繰り返すが、リストには要素の順序があり、そして重複を許すトコにある。言い換えると問題に適したデータ型を使わないと問題が難しくなる、と言う典型例だ、って事なんだ。それが簡単な問題を超難問化させる原因だ。
いずれにせよ、上のコードがどうなるのかテストしてみよう。
> (combination (set 'A 'B 'C 'D) 2)
(set (set 'B 'D) (set 'C 'B) (set 'A 'D) (set 'C 'A) (set 'B 'A) (set 'C 'D))
>
と、確かにパスカルの三角形が表すような結果を得ることが出来る。
万歳!
とは言っても、ここまでロジックを解き明かすと、「あれ?このままリストに置き換えても良くね?」と思うだろう。
どうなんだかちと確かめてみよう。
(define (combination xs r)
(cond ((zero? r) '(()))
((= r (length xs)) `(,xs))
(else (let ((s (cdr xs)))
`(,@(map (lambda (x)
(cons (car xs) x)) (combination s (- r 1)))
,@(combination s r))))))
基本、集合を使った関数の内部で使われてる関数を置き換え直しただけ、だ。
これを使って結果がどうなるか確かめてみよう。
> (combination '(A B C D) 2)
'((A B) (A C) (A D) (B C) (B D) (C D))
>
なんとこれでも上手く行ってるのだ(笑)。
そう、リストを使うから再帰の構造がどうなんだ、って悩むが、一旦集合を経過して見直してみると、さして難しくはない、むしろ疑問が氷解してる事に気づくだろう(※2)。
実はこの再帰関数を理解する為にはトレースをかけてみてもダメなんだ。そうじゃなくってちょっとした数学、もっと言っちゃうとパスカルの三角形の性質を上手く利用して、そっちを経由して理解するのが正解なんだ。
今までの、両替の問題、そして順列は「再帰の枠組みで再帰を理解する」、つまりあくまでもプログラミングテクニックの延長線上での理解で間に合うが、一方、この問題の難しさ、は「数学の仕組みで再帰を理解しないといけない」、ある意味直球勝負のトコに由来する。
多分この問題は、数学自体をちょっとは使わなければ理解しづらい、と言うのがハードルを上げる一因にはなっている。逆に言うとこの問題は、数学を避けずに数学そのものとして捉えた方がむしろ簡単になるんだ。レアケースだけどね(※3)。
最後に、計算効率を考慮して、遅延リスト版も紹介しておこう。
(define (stream-combination strm r)
(cond ((zero? r) (stream stream-null))
((= r (stream-length strm)) (stream strm))
(else (let ((s (stream-cdr strm)))
(stream-append
(stream-map (lambda (x)
(stream-cons (stream-car strm) x))
(stream-combination s (- r 1)))
(stream-combination s r))))))
参考: 今回のソースコード
※1: ∪ は集合の和、を示す。言い換えると集合同士の「足し算」を現し、普通の数値同士の計算では+と意味的には同じだ。
違うトコは、繰り返すが、集合は「重複を許さない」ので、同じ要素が複数あった場合、プログラム的には「1つを残して削除する」と言う作用がある。
※2: 集合を用いた「組み合わせ」とリストを用いた「組み合わせ」で唯一計算が違うのは、次のような計算をする時、答えがどうなるか、だ。
(combination (set 'A 'A 'A 'A) 2)(combination '(A A A A) 2)
前者はエラーを返し、後者は'((A A) (A A) (A A) (A A) (A A) (A A))を返すだろう。
一体どっちが正しいのか、と言うと、数学的には前者となる。何故なら組み合わせで扱う要素は「互いに識別可能だ」と言う前提があり、集合として考えると{A, A, A, A}と言う組は{A}へと縮む。
一方リスト版はその辺を全く考慮していない。機械的に再帰を実行してるだけ、だ。
※3: とここまで来て、理解してくれた方々には真に申し訳ないが、Racketにも組み込みで組み合わせとしてのリストを返す関数(combinations)がある。
一方、permutationsと名付けられた関数も存在はするが、例えば長さがnのリストだとnからn選ぶ順列しか得られない。
よって、自作するならnからk選ぶ順列の方、となる。















