
世紀の7大難問のうちの1つである「ポアンカレ予想」という位相幾何学(トポロジー)の問題を証明したとして2006年にペレリマンというロシアの天才数学者がフィールズ賞を受賞した。4年に1度、数学の分野で功績を残した人に与えられる栄誉ある賞だ。
しかし、ペレリマンは受賞を辞退し賞金100万ドルを受け取らなかったばかりでなく、数学の世界から身を引いて隠遁生活に入ってしまった。理由は誰にもわからない。彼は若干40歳である。
およそ100年間数学者を悩ませてきた「ポアンカレ予想」とペレリマンをテーマに、先日NHK BSで「数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」という番組が放送された。(地上波デジタルではそのダイジェスト版が放送された。)
今回僕が読んだ「トポロジカル宇宙(完全版):根上生也著」はペレリマンが証明したという事実を補って「完全版」として改訂されたばかりのトポロジー(位相幾何学)の入門書だ。数式はいっさいでてこない一般向けに書かれた「超入門書」といってよい。本の帯には『ペレルマンは、どうやって「ポアンカレ予想」を完全解決したのか? - その全行程を、数式を使わずていねいに描き出す。』とある。
これまで何冊かトポロジーの入門書を手にとってみたが、これほど入りやすい本はなかった。トーラスと呼ばれるドーナツの形をはじめとするいろいろな形の研究がどうして大切な学問なのか、数学とは無縁な人にも納得できるように、そして生き生きと書かれている。
ドーナツとコーヒーカップが同じ形に分類されると言われても、僕はちっとも面白くなかったのだが、この本を読んでがぜん興味がわいてきた。僕たちは3次元空間の内部に住んでいるために直接見ることのできない宇宙空間全体の形、4次元以上の空間の形や性質も位相幾何学使えば研究できるのだ。著者はこの分野の専門家なのでたとえ「たとえ話」であっても正確さはほとんど損なわれていない。
しかし、これを読んだからと言ってペレリマンの証明が理解できるようになるわけではない。(それは都合よすぎる!)位相幾何学(トポロジー)の専門家でさえ、彼の証明が正しいことがわかるまで4年もの検証が必要だったのだから、凡人に理解させるような本は無理というものだ。少なくともトポロジーとはどのような学問か?ポアンカレ予想とはどのような問題かという点について想像できるようになるだけでも、数学と無縁だった者にはうれしいはずだ。
さて「ポアンカレ予想」であるが言葉で書くと「単連結な3次元閉多様体は3次元球面と同相と言えるか?」となる。地球の表面は「2次元球面」であるから「3次元球面」とはそれより1次元多い立体球面ということだ。つまり4次元球の「3次元表面」だ。ポアンカレ予想を式で書くとこのようになる。
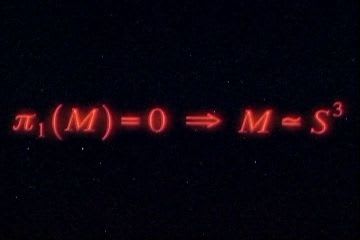
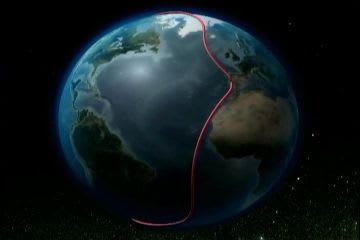
次元を1つ少なくした2次元球面の場合、つまり地球の表面を例にとって考える。16世紀にマゼランは船でポルトガルから西へ西へと進み、地球を一周した。地球が丸いことを身をもって証明したとされるのだが、400年後フランスの数学者であるポアンカレが、それでは証明になっていないことを主張した。彼のアイデアによれば船にロープをつけて地球を一周して戻ってきたとき、この図のようにロープをたぐり寄せることができれば地球は丸いということがわかる。ただし、ロープは地表面から離れてはいけない。(2次元球面内にロープが常にあるようにする。)
しかし、もし地球が下の図のようにドーナツ型をしていたら、船は一周して戻ってくることができるにもかかわらずロープをたぐり寄せることはできない。だからマゼランの方法では証明になっていないと主張したのだ。ドーナツの形をしていたとしても地球表面の2次元空間しか移動できない人間には直接穴を見ることができないが、ロープがたぐり寄せられないことから穴の存在を確認できる。これがキーポイントだ。
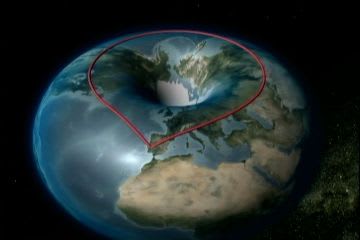
この地球が(ドーナツでなく)丸い場合が2次元の場合の「ポアンカレ予想」に相当する。つまり「単連結な二次元閉多様体は二次元球面と同相と言える。」のだ。
同じ問題を宇宙という3次元の空間について考えたのが本来の「ポアンカレ予想」だ。広大な宇宙は外から見ることはできないし、仮に「外」があったとしたらその場所も宇宙の一部なので「外」ではなくなってしまう。宇宙全体を見るためには宇宙を含んでいる4次元空間から見るしかない。それはちょうど私達の3次元空間が2次元の平面を含んでいるのと同じである。
問題の難しさは宇宙の中にいながら、宇宙全体の形を知ることができるかという点だ。少なくとも2次元の場合1本のロープをたぐり寄せられるかということによって「穴があるかないか」がわかったのだが、同じ手法が3次元でも通用するだろうというのが「ポアンカレ予想」である。ロープをつけたロケットを地球から発射して宇宙を一周して地球に戻ってきたとき、ロープがたぐり寄せられれば「宇宙は丸い」ということになる。たぐり寄せられなければ「宇宙にはドーナツのように穴が開いている。」わけだ。
ところでNHKの番組で用いられていた以下の図や説明なのだが、不正確であることに気がついた。一般向けの番組なので、正確に説明して内容がわかりにくくなるのを避けたのだと思う。

宇宙を一周させたロープを描いた図なのだが「宇宙は丸い」という正確な意味を伝えていない。マゼランは西へ西へと航海した。地球が丸いから、つまり地表面が曲がっているから船は出発した方向と反対の東側から戻ってきたわけだ。
つまり3次元の宇宙空間を飛ぶロケットもずっと真っ直ぐに飛び続けなければいけない。もし「宇宙が丸い」とすると出発した方向とは反対側から地球に戻ってこなければならない。つまり真っ直ぐだと思って進んでも空間が曲がっているからぐるりとひと回りして戻ってくるわけだ。上に向かってロケットを打ち上げれば地面の下方向から戻ってくるし、東に向かって飛ばせば西から戻ってくる。そのようなことが図では表現できていないし、説明からも省かれている。「宇宙が丸い」とは宇宙空間が曲がっていいるから、まっすぐに進んでいっても元の場所に戻ってきてしまうという意味だ。
そのような背景知識を前提に次の「宇宙に穴が開いている場合」の図をご覧になるとよい。この場合、ロープはたぐり寄せることができない。

「ポアンカレ予想」はおよそ100年の間、数学者を悩ませ続けてきた。この問題に取り組んだために人生を台無しにした数学者が何人も出た。「ポアンカレ予想」には人を虜にしてしまう魔力があったのである。しかし3次元多様体の問題であるのに、より高い次元の問題のほうが易しく、6次元、5次元、4次元の順に証明が見つかったのである。
1982年にアメリカのサーストンという数学者が「サーストンの幾何化予想」というものすごいアイデアを打ち立てた。「三次元多様体は一様な幾何構造の断片に分解できるだろう」というもので、宇宙を構成する空間の断片がこの図で示されているような最大8種類の形に限られていることを示した。サーストンはこれを証明したわけではない。ともかく物理学のように実験や観察で検証したわけでもないのに、頭の中の数学だけで宇宙の形の8種類の可能な断片を導きだしたことは他の数学者にとっても大きな驚きであった。これらがその8種類の形である。
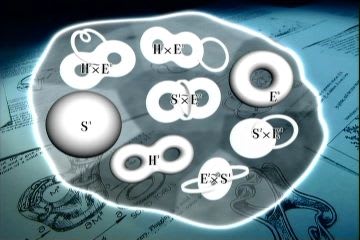
これには「丸い宇宙」も含まれているから、ロープをかけてたぐり寄せられればそれ以外の形の断片は存在していないことになるので、「サーストンの幾何化予想」が証明されれば、同時にポアンカレ予想も証明されたことになる。「サーストンの幾何化予想」は「ポアンカレ予想」を含んでいる。
ちなみに「サーストンの幾何化予想」がどのようなものであるかは「低次元の幾何からポアンカレ予想へ : 市原一裕」をお読みになるとよい。
ペレリマンは物理の方程式である「リッチフロー方程式」を使えば「サーストンの幾何化予想」をが証明できることに気がついた。そして2002年と2003年に「リッチフローの三次元多様体への応用」という論文をインターネット上の非公式論文サイトに掲載した。これである。
当初、これが「ポアンカレ予想」の証明になっていると誰も信じなかった。間違った論文が多数掲載されていたからである。2004年にペレリマンはアメリカのプリンストン大学に招かれ、100名以上の位相幾何学の専門家や数学者の前でその説明を行った。しかし会場にいた数学者は誰も彼の説明を理解することができなかった。それは「ポアンカレ予想」は位相幾何学の問題であったにもかかわらず、ペレリマンが彼の専門分野である微分幾何学や、数学では全く使わない物理学の概念や手法を駆使して証明したからだ。
位相数学者たちは3つの意味で落胆した。1つは自分が人生をかけて挑んできたポアンカレ予想が証明され、目標を失ったこと。もう1つはその証明が位相幾何学ではない手法で解かれたこと、最後にその証明が自分には全く理解できなかったことだ。
数学者たちによる4年による精査の結果、ペレリマンの証明が正しいことが最終的に認められた。
ちなみに、ペレリマンが2002年と2003年に「リッチフローの三次元多様体への応用」として掲載した論文は一般公開されている。以下のアドレスをクリックするとPDFで読むことができる。
http://arxiv.org/find/all/1/au:+Perelman_Grisha/0/1/0/all/0/1
ペレリマンによる論文ではないが「リッチフローによるポアンカレ予想と幾何化予想の完全な証明」も以下のPDFファイルで読める。(こちらは328ページもある)
http://www.ims.cuhk.edu.hk/~ajm/vol10/10_2.pdf
なお、今回記事として紹介した後半はは主にNHKの番組で「トポロジカル宇宙(完全版):根上生也著」の内容ではないことをおことわりしておく。




余談:ペレリマンの日本語表記を本では「ペレルマン」としている。NHKの番組では「ペレリマン」だ。これは彼の名前の英語表記(Perelman)をもとにすれば「ペレルマン」で、ロシア語表記をもとにすれば「ы=ィ」の音が入るので「ペレリマン」となる。
最後に「トポロジカル宇宙(完全版):根上生也著」の内容を目次で紹介しておく。
第1章:宇宙の形とは?
七次元人との会見
二次元人の悲劇
果てがないのに有限!
各人が天球を持っている
百億のニューロンたちよ!
第2章:丸い宇宙とは?
大航海時代を経て
宇宙が丸いということは
二つの天球を持つ宇宙
コンパスが描く宇宙
四次元空間を見る
三次元球面宇宙の正体
新たな旅立ちへ
第3章:宇宙儀製造計画
宇宙儀を作ろう
宇宙を縮小する
なぜ地球儀は机の上にあるのか
宇宙の展開図を作る
トーラス宇宙の場合
宇宙を半分にする
宇宙儀の完成
第4章:第ニ期大航海時代
思考エンジン、始動!
地球は本当に丸かったのか?
空間に開いた穴
ブラックホールに突入!
見えない穴の正体
消滅する宇宙の穴
宇宙の形の判定
第5章:そして、宇宙の果てへ
初めて日本の形を見た男
宇宙に潜む流れを探せ!
たばたば空間の拡大
繰り返しの宇宙
エッシャー宇宙
宇宙の果てはトーラスだった
君も、間宮林蔵となれ!
第6章:第ニ千年紀を迎えて
ポアンカレ予想が解けた!
数学は生きている
フィールズ賞とミレニアム懸賞問題
空間の曲率を均していくと
特異点を手術する
最終到達地点
封印の章
七次元人の残した言葉
三次元宇宙を七次元宇宙に納める
新たな覚醒を目指して
注:この記事で使用した7枚の図はNHKの番組の録画データから拝借しました。これらの著作権はNHKにあります。
しかし、ペレリマンは受賞を辞退し賞金100万ドルを受け取らなかったばかりでなく、数学の世界から身を引いて隠遁生活に入ってしまった。理由は誰にもわからない。彼は若干40歳である。
およそ100年間数学者を悩ませてきた「ポアンカレ予想」とペレリマンをテーマに、先日NHK BSで「数学者はキノコ狩りの夢を見る ~ポアンカレ予想・100年の格闘~」という番組が放送された。(地上波デジタルではそのダイジェスト版が放送された。)
今回僕が読んだ「トポロジカル宇宙(完全版):根上生也著」はペレリマンが証明したという事実を補って「完全版」として改訂されたばかりのトポロジー(位相幾何学)の入門書だ。数式はいっさいでてこない一般向けに書かれた「超入門書」といってよい。本の帯には『ペレルマンは、どうやって「ポアンカレ予想」を完全解決したのか? - その全行程を、数式を使わずていねいに描き出す。』とある。
これまで何冊かトポロジーの入門書を手にとってみたが、これほど入りやすい本はなかった。トーラスと呼ばれるドーナツの形をはじめとするいろいろな形の研究がどうして大切な学問なのか、数学とは無縁な人にも納得できるように、そして生き生きと書かれている。
ドーナツとコーヒーカップが同じ形に分類されると言われても、僕はちっとも面白くなかったのだが、この本を読んでがぜん興味がわいてきた。僕たちは3次元空間の内部に住んでいるために直接見ることのできない宇宙空間全体の形、4次元以上の空間の形や性質も位相幾何学使えば研究できるのだ。著者はこの分野の専門家なのでたとえ「たとえ話」であっても正確さはほとんど損なわれていない。
しかし、これを読んだからと言ってペレリマンの証明が理解できるようになるわけではない。(それは都合よすぎる!)位相幾何学(トポロジー)の専門家でさえ、彼の証明が正しいことがわかるまで4年もの検証が必要だったのだから、凡人に理解させるような本は無理というものだ。少なくともトポロジーとはどのような学問か?ポアンカレ予想とはどのような問題かという点について想像できるようになるだけでも、数学と無縁だった者にはうれしいはずだ。
さて「ポアンカレ予想」であるが言葉で書くと「単連結な3次元閉多様体は3次元球面と同相と言えるか?」となる。地球の表面は「2次元球面」であるから「3次元球面」とはそれより1次元多い立体球面ということだ。つまり4次元球の「3次元表面」だ。ポアンカレ予想を式で書くとこのようになる。
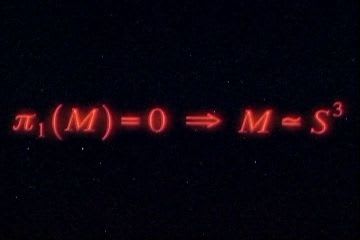
次元を1つ少なくした2次元球面の場合、つまり地球の表面を例にとって考える。16世紀にマゼランは船でポルトガルから西へ西へと進み、地球を一周した。地球が丸いことを身をもって証明したとされるのだが、400年後フランスの数学者であるポアンカレが、それでは証明になっていないことを主張した。彼のアイデアによれば船にロープをつけて地球を一周して戻ってきたとき、この図のようにロープをたぐり寄せることができれば地球は丸いということがわかる。ただし、ロープは地表面から離れてはいけない。(2次元球面内にロープが常にあるようにする。)

しかし、もし地球が下の図のようにドーナツ型をしていたら、船は一周して戻ってくることができるにもかかわらずロープをたぐり寄せることはできない。だからマゼランの方法では証明になっていないと主張したのだ。ドーナツの形をしていたとしても地球表面の2次元空間しか移動できない人間には直接穴を見ることができないが、ロープがたぐり寄せられないことから穴の存在を確認できる。これがキーポイントだ。

この地球が(ドーナツでなく)丸い場合が2次元の場合の「ポアンカレ予想」に相当する。つまり「単連結な二次元閉多様体は二次元球面と同相と言える。」のだ。
同じ問題を宇宙という3次元の空間について考えたのが本来の「ポアンカレ予想」だ。広大な宇宙は外から見ることはできないし、仮に「外」があったとしたらその場所も宇宙の一部なので「外」ではなくなってしまう。宇宙全体を見るためには宇宙を含んでいる4次元空間から見るしかない。それはちょうど私達の3次元空間が2次元の平面を含んでいるのと同じである。
問題の難しさは宇宙の中にいながら、宇宙全体の形を知ることができるかという点だ。少なくとも2次元の場合1本のロープをたぐり寄せられるかということによって「穴があるかないか」がわかったのだが、同じ手法が3次元でも通用するだろうというのが「ポアンカレ予想」である。ロープをつけたロケットを地球から発射して宇宙を一周して地球に戻ってきたとき、ロープがたぐり寄せられれば「宇宙は丸い」ということになる。たぐり寄せられなければ「宇宙にはドーナツのように穴が開いている。」わけだ。
ところでNHKの番組で用いられていた以下の図や説明なのだが、不正確であることに気がついた。一般向けの番組なので、正確に説明して内容がわかりにくくなるのを避けたのだと思う。

宇宙を一周させたロープを描いた図なのだが「宇宙は丸い」という正確な意味を伝えていない。マゼランは西へ西へと航海した。地球が丸いから、つまり地表面が曲がっているから船は出発した方向と反対の東側から戻ってきたわけだ。
つまり3次元の宇宙空間を飛ぶロケットもずっと真っ直ぐに飛び続けなければいけない。もし「宇宙が丸い」とすると出発した方向とは反対側から地球に戻ってこなければならない。つまり真っ直ぐだと思って進んでも空間が曲がっているからぐるりとひと回りして戻ってくるわけだ。上に向かってロケットを打ち上げれば地面の下方向から戻ってくるし、東に向かって飛ばせば西から戻ってくる。そのようなことが図では表現できていないし、説明からも省かれている。「宇宙が丸い」とは宇宙空間が曲がっていいるから、まっすぐに進んでいっても元の場所に戻ってきてしまうという意味だ。
そのような背景知識を前提に次の「宇宙に穴が開いている場合」の図をご覧になるとよい。この場合、ロープはたぐり寄せることができない。

「ポアンカレ予想」はおよそ100年の間、数学者を悩ませ続けてきた。この問題に取り組んだために人生を台無しにした数学者が何人も出た。「ポアンカレ予想」には人を虜にしてしまう魔力があったのである。しかし3次元多様体の問題であるのに、より高い次元の問題のほうが易しく、6次元、5次元、4次元の順に証明が見つかったのである。
1982年にアメリカのサーストンという数学者が「サーストンの幾何化予想」というものすごいアイデアを打ち立てた。「三次元多様体は一様な幾何構造の断片に分解できるだろう」というもので、宇宙を構成する空間の断片がこの図で示されているような最大8種類の形に限られていることを示した。サーストンはこれを証明したわけではない。ともかく物理学のように実験や観察で検証したわけでもないのに、頭の中の数学だけで宇宙の形の8種類の可能な断片を導きだしたことは他の数学者にとっても大きな驚きであった。これらがその8種類の形である。

これには「丸い宇宙」も含まれているから、ロープをかけてたぐり寄せられればそれ以外の形の断片は存在していないことになるので、「サーストンの幾何化予想」が証明されれば、同時にポアンカレ予想も証明されたことになる。「サーストンの幾何化予想」は「ポアンカレ予想」を含んでいる。

ちなみに「サーストンの幾何化予想」がどのようなものであるかは「低次元の幾何からポアンカレ予想へ : 市原一裕」をお読みになるとよい。
ペレリマンは物理の方程式である「リッチフロー方程式」を使えば「サーストンの幾何化予想」をが証明できることに気がついた。そして2002年と2003年に「リッチフローの三次元多様体への応用」という論文をインターネット上の非公式論文サイトに掲載した。これである。
当初、これが「ポアンカレ予想」の証明になっていると誰も信じなかった。間違った論文が多数掲載されていたからである。2004年にペレリマンはアメリカのプリンストン大学に招かれ、100名以上の位相幾何学の専門家や数学者の前でその説明を行った。しかし会場にいた数学者は誰も彼の説明を理解することができなかった。それは「ポアンカレ予想」は位相幾何学の問題であったにもかかわらず、ペレリマンが彼の専門分野である微分幾何学や、数学では全く使わない物理学の概念や手法を駆使して証明したからだ。
位相数学者たちは3つの意味で落胆した。1つは自分が人生をかけて挑んできたポアンカレ予想が証明され、目標を失ったこと。もう1つはその証明が位相幾何学ではない手法で解かれたこと、最後にその証明が自分には全く理解できなかったことだ。
数学者たちによる4年による精査の結果、ペレリマンの証明が正しいことが最終的に認められた。
ちなみに、ペレリマンが2002年と2003年に「リッチフローの三次元多様体への応用」として掲載した論文は一般公開されている。以下のアドレスをクリックするとPDFで読むことができる。
http://arxiv.org/find/all/1/au:+Perelman_Grisha/0/1/0/all/0/1
ペレリマンによる論文ではないが「リッチフローによるポアンカレ予想と幾何化予想の完全な証明」も以下のPDFファイルで読める。(こちらは328ページもある)
http://www.ims.cuhk.edu.hk/~ajm/vol10/10_2.pdf
なお、今回記事として紹介した後半はは主にNHKの番組で「トポロジカル宇宙(完全版):根上生也著」の内容ではないことをおことわりしておく。




余談:ペレリマンの日本語表記を本では「ペレルマン」としている。NHKの番組では「ペレリマン」だ。これは彼の名前の英語表記(Perelman)をもとにすれば「ペレルマン」で、ロシア語表記をもとにすれば「ы=ィ」の音が入るので「ペレリマン」となる。
最後に「トポロジカル宇宙(完全版):根上生也著」の内容を目次で紹介しておく。
第1章:宇宙の形とは?
七次元人との会見
二次元人の悲劇
果てがないのに有限!
各人が天球を持っている
百億のニューロンたちよ!
第2章:丸い宇宙とは?
大航海時代を経て
宇宙が丸いということは
二つの天球を持つ宇宙
コンパスが描く宇宙
四次元空間を見る
三次元球面宇宙の正体
新たな旅立ちへ
第3章:宇宙儀製造計画
宇宙儀を作ろう
宇宙を縮小する
なぜ地球儀は机の上にあるのか
宇宙の展開図を作る
トーラス宇宙の場合
宇宙を半分にする
宇宙儀の完成
第4章:第ニ期大航海時代
思考エンジン、始動!
地球は本当に丸かったのか?
空間に開いた穴
ブラックホールに突入!
見えない穴の正体
消滅する宇宙の穴
宇宙の形の判定
第5章:そして、宇宙の果てへ
初めて日本の形を見た男
宇宙に潜む流れを探せ!
たばたば空間の拡大
繰り返しの宇宙
エッシャー宇宙
宇宙の果てはトーラスだった
君も、間宮林蔵となれ!
第6章:第ニ千年紀を迎えて
ポアンカレ予想が解けた!
数学は生きている
フィールズ賞とミレニアム懸賞問題
空間の曲率を均していくと
特異点を手術する
最終到達地点
封印の章
七次元人の残した言葉
三次元宇宙を七次元宇宙に納める
新たな覚醒を目指して
注:この記事で使用した7枚の図はNHKの番組の録画データから拝借しました。これらの著作権はNHKにあります。





















お仕事忙しいそうですが、寝る間も削って、書かれているのではないですか?
岩波の理工系の基礎数学の「微分・位相幾何」は、入門するのには、敷居が低くて良いのかも知れませんが、数学的なレヴェルは低いですよ。
むしろ、易しいことしか書かれていないように一見見える、東京大学出版会の「多様体の基礎」を、丁寧に読んでいった方が、後々のためになると思います。この本は、本当に、読者のことを考えて、書かれているからです。もっと難しい、裳華房の「多様体入門」(松島与三)や、岩波の「位相幾何学Ⅰ」なんかを読む前に、この本を読んでおくことで、つまらないぬかるみに足を取られることを避けられるのです。
回り道をしたら、それだけの甲斐は必ずあるものです。
量子力学の勉強をする時、朝永の量子力学を読んだ時のことを思い出して下さい。
> 立派な記事ですね。時間をかけて、
> 書かれたのだろうなと、感心させられました。
照れてしまいますね。ありがとうございます。NHKの番組については記事にしてみたかったので、少しずつ書きためていたのです。そのまま記事にすると単なる受け売りになりそうでしたので、本のレビューにかれめて書きました。
「多様体の基礎」をアマゾンで検索してみました。たくさんの方がレビューを書かれていましたが、よさそうな本ですね。週末にジュンク堂に行って実物を見てみます。ご紹介いただきありがとうございました。
「微分・位相幾何」のほうも読み進めているうちにEROICAさんがおっしゃっている通りだなと思いました。証明抜きにざっと概要をつかむための本で、かなり物理学を意識していますね。
数学は「寄り道」のつもりでしたが、寄り道ついでにもう少し奥へ進んでみようかと思います。(まだ積読状態の物理の本が数冊待ってるんですけどね。)
会社のプリンターでこっそり出力しました。持ち帰って読んでみます。
(たぶん、挫折すると思います。)
ちなみに「トポロジカル宇宙(旧版)」もBook Offで105円で買いました。
こちらこそ、お久しぶりです。
論文をプリントされたのですね!
> (たぶん、挫折すると思います。)
おそらくそうなることでしょう。。。。
> ちなみに「トポロジカル宇宙(旧版)」も
> Book Offで105円で買いました。
な、なんと105円!?ラッキーですね。
僕は定価で買ってしまいました!Book Offは高校1年になる甥の学習参考書などを買うときなど時々利用しています。まったく勉強しない子なので、新品の本を与えるのは無駄になるかと。。。案の定、参考書は開いてもいないようです。
NHKに限らず、地上波のゴールデンタイムにこのような良質の番組がもっと放送されるようになればいいのにと思っています。
拙著について,とてもすてきなコメントを書いていただき,感激です.ありがとうございます.
実は,NHKスペシャルの番組の制作にも関わっていました.
はじめまして。わざわざコメントいただき僕のほうこそ感激しております。ありがとうございました。
先生がNHKスペシャルの番組の監修をされていたことも、ブログのこの記事を書いてからしばらくして気がつきました。
「トポロジカル宇宙」は本当に楽しく読ませていただきました。「理系離れ」が憂慮されている昨今、理系科目への「動機付け」となるこのような本がたくさん出版されればよいと思っています。と同時にゴールデンタイムに良質な科学番組がもっと放送されるようになればとも。。。
先生のHPも拝見させていただきました。専門分野のお仕事と入門書の執筆など、大変お忙しいと思いますが、今後も両方の分野でますますご活躍いただきたいと思っております。