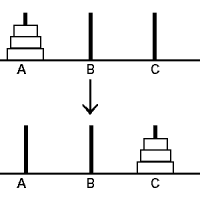
すこしずつ一般化した場合を考えてみます。
最適なxがただ一つに決まらない場合について考えたいと思います。つまり、x(x+1)/2<n<(x+1)(x+2)/2のときです。このときの最適な分割数はx or x+1となります。
b(n)=2b(n-x)+a(x)
この漸化式を解くわけですが、問題はb(n-x)にあります。n<(x+1)(x+2)/2ですから、(x+1)(x+2)/2-n=k(整数)とおくと、
x(x+1)/2-(n-x)=k-1
となって、しまいますから、この漸化式を一度使うたびごとに、上側の値に近づいていくことになります。例えば、n=8のときには、x=3です。このとき、(x+1)(x+2)/2=10ですから、10-8=2回漸化式で変換すると、前回特別な形になります。実際、
b(8)=2b(5)+a(3)=2(2b(3)+a(2))+a(3)=4b(3)+a(3)+2a(2)
で、このb(3)は前回の特別な形の場合b'(2)になります。
このことをまとめると、(x+1)(x+2)/2-n=kとおいたとき、
b(n)=2^k b(n-x-(x-1)-...-(x-k+1))+a(x)+2a(x-1)+...+2^(k-1) a(x-k+1)
となって、n-x-(x-1)-...-(x-k+1)=(x-k+1)(x-k+2)/2を満たしますから、
b(n)=2^k b'(x-k+1)+a(x)+2a(x-1)+...+2^(k-1) a(x-k+1)
となります。ここで、a(x)=2^x-1, b'(x)=(x-1) 2^x+1を代入して整理すれば、
b(n)=(2x-k) 2^x+1
となります。実際、n=8のときにはx=3, k=2でしたから、
b(8)=(2×3-2)×2^3+1=4×8+1=33
となって、あっています。
同様に、x+1を使った場合を考えれば、n-x(x+1)/2=mとおくと
(n-(x+1))-x(x-1)/2=m-1
となりますから、1回ごとに下の値に近づいていることがわかります。したがって
b(n)=2^k b(n-(x+1)-x-...-(x-m+2))+a(x+1)+2a(x)+...+2^(m-1) a(x-m+2)
となって、n-(x+1)-x-...-(x-m+2)=(x-m)(x-m+1)/2を満たしますから、
b(n)=2^m b'(x-m)+a(x+1)+2a(x)+...+2^(m-1) a(x-m+2)
となります。ここで、a(x)=2^x-1, b'(x)=(x-1) 2^x+1を代入すれば、
b(n)=(x+m-1) 2^x+1
となります。実際、n=8のときにはx=3, m=2でしたから、
b(8)=(3+2-1)×2^3+1=4×8+1=33
となって、あっています。
これでなんとか式ができたようです。
続きは次回に
最適なxがただ一つに決まらない場合について考えたいと思います。つまり、x(x+1)/2<n<(x+1)(x+2)/2のときです。このときの最適な分割数はx or x+1となります。
この漸化式を解くわけですが、問題はb(n-x)にあります。n<(x+1)(x+2)/2ですから、(x+1)(x+2)/2-n=k(整数)とおくと、
x(x+1)/2-(n-x)=k-1
となって、しまいますから、この漸化式を一度使うたびごとに、上側の値に近づいていくことになります。例えば、n=8のときには、x=3です。このとき、(x+1)(x+2)/2=10ですから、10-8=2回漸化式で変換すると、前回特別な形になります。実際、
b(8)=2b(5)+a(3)=2(2b(3)+a(2))+a(3)=4b(3)+a(3)+2a(2)
で、このb(3)は前回の特別な形の場合b'(2)になります。
このことをまとめると、(x+1)(x+2)/2-n=kとおいたとき、
b(n)=2^k b(n-x-(x-1)-...-(x-k+1))+a(x)+2a(x-1)+...+2^(k-1) a(x-k+1)
となって、n-x-(x-1)-...-(x-k+1)=(x-k+1)(x-k+2)/2を満たしますから、
b(n)=2^k b'(x-k+1)+a(x)+2a(x-1)+...+2^(k-1) a(x-k+1)
となります。ここで、a(x)=2^x-1, b'(x)=(x-1) 2^x+1を代入して整理すれば、
b(n)=(2x-k) 2^x+1
となります。実際、n=8のときにはx=3, k=2でしたから、
b(8)=(2×3-2)×2^3+1=4×8+1=33
となって、あっています。
同様に、x+1を使った場合を考えれば、n-x(x+1)/2=mとおくと
(n-(x+1))-x(x-1)/2=m-1
となりますから、1回ごとに下の値に近づいていることがわかります。したがって
b(n)=2^k b(n-(x+1)-x-...-(x-m+2))+a(x+1)+2a(x)+...+2^(m-1) a(x-m+2)
となって、n-(x+1)-x-...-(x-m+2)=(x-m)(x-m+1)/2を満たしますから、
b(n)=2^m b'(x-m)+a(x+1)+2a(x)+...+2^(m-1) a(x-m+2)
となります。ここで、a(x)=2^x-1, b'(x)=(x-1) 2^x+1を代入すれば、
b(n)=(x+m-1) 2^x+1
となります。実際、n=8のときにはx=3, m=2でしたから、
b(8)=(3+2-1)×2^3+1=4×8+1=33
となって、あっています。
これでなんとか式ができたようです。
続きは次回に