ノート

趣味で物理を勉強して、できたノート。

虚数

2009年12月20日 | 特殊相対性理論
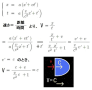
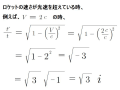最高速度を不変にすると、それを超えた時の時間は「解なし」になる。

中学では「解なし」だったけど、「解あり」だとするとタイムマシンに乗ってる時の時間は虚数倍になっている。


虚数は二つをうまくかければ、虚数ではなくなる。
量子力学では虚数を使った数学を使うと計算が楽になるようだ。



理科

2009年11月10日 | 特殊相対性理論
Texソフトがなんとか回復しました。

引き続き、概要を続けてゆきたいと思います。

ですが、今回は休息して未来の高校受験問題を考察した。

公立校の理科の問題。義務教育に移行することは、はたしてできるか・・・

速度の合成

2009年09月01日 | 特殊相対性理論
速度の合成が普通の足し算ではなくなる。

普通の足し算だと簡単に光速を超える速さが書けていたけれど、これだと大丈夫だ。

もし太陽が無くなっても地球では８分は気付かないし、引力も光速を超えないので８分は太陽があった周りをのん気に回るようだ。





運動量Ｐ

2009年08月27日 | 特殊相対性理論
エネルギーの式を眺めてて、ふと浮かんだ絵。
あ、Ｐは運動量（質量×速度）です。書き忘れてました。
空間は１から３と書き、時間は４番目と書かず０番目と書いている。
ＥはＰの０番目って感じです。


ノートが停滞中、というか最近は「選挙どうしようかな」とか思ってる。
でも、はっきり言ってよくわからなくて決断できてませんけど。


速度合成の数式をＴＥＸで作成中・・・。

不変量（修正）

2009年08月22日 | 特殊相対性理論
４次元の不変量（ローレンツ不変）からＥなどが導けて、こんな感じで書かれている。

５次元の理論も考えられている。
変数Yは宇宙の外側の空間のようだ。
重力が磁力などよりも小さいのは重力の一部が宇宙の外側へ漏れているからだという理論がある。（ランドール・サンドラムのモデル）

今年にＣＥＲＮの衝突実験でミニブラックホールができれば、この５次元理論は正しいという話もある。

（追記）
η（エータ）は計量と呼ばれています。

-------------訂正---------------------

「縮約」は内積やスカラーと呼ばれる数字（方向を持たない、座標変換に対して不変）などに使われ、総和（Σ）を省略するのは「略記」でした。

Σ　をいっぱい書くことになるので面倒だという理由のようです。



電磁波

2009年08月16日 | 特殊相対性理論
逆に、電磁気を４つにまとめたマクスウェル方程式から、ローレンツ不変、ローレンツ変換と導出できる。
歴史的にはそうらしい。

電磁気の式は時間を絶対にしたガリレイ変換では不変にならない。
光も赤外線などの電磁波の一種なので、なんとなくつながりが見えてスッキリしたよ。






逆行列のとこ

2009年08月08日 | 特殊相対性理論
私は高校３年生で習った。

３行３列の逆行列は数学の専門書に書いてあるけれど、今の場合は時間と空間１次元なので２行２列の逆行列で計算できる。

２行２列の逆行列は、たぶん高校数３の教科書に書いてあるので、暗記だけどコレの場合は形をそのまま覚えた方がよさそう。



ローレンツ変換

2009年07月31日 | 特殊相対性理論
速度をもつことによって、時間や長さ等がどうなるかはコレを計算すれば出てくるよ。

３つの条件からa,b,e,fの定数のうちの３つが求まる。
残りのひとつは、２つの座標が互いに(v)と(-v)の関係にあることから求まる。
絶対的基準がどちらかではなく、２つの相対性を調べて求める。




Ｅ＝

2009年07月08日 | 特殊相対性理論
ちょっとけずった。いや、かなりけずった。

ｃの3乗とかだったら原子力発電も助かるのに・・・

ところで３乗の式とかあるみたいだけど、フェルマーの最終定理というやつで解が無いらしい。だから三立方は無しかも。

三平方から三立方を飛び越えて四立方、それで発電量は2倍。
この場合、反ウランで発電・・・。
とりあえず言ってみたかった。

----------------------------------
次元解析で言うと、
三角形の三辺の距離 x=vt,ct,cTの単位はどれも(m)で同じなので、加速度×距離の単位は(m/s^2)×m=(m^2/s^2)=(m/s)^2となり、速度の２乗の形にできる。
なので、ax=c^2 に変わる。

２

2009年07月04日 | 特殊相対性理論
（微分の式は記事「累乗の微分」を参考にしてね）

右辺のＣの２乗がエネルギーの式の最後にも出てくる。

止まっている時の質量はm0です。

中学の時からのプラスとマイナスの２つの組み合わせが不思議に思えたりもするなぁ。

その他の、３乗、４乗とか、虚数乗とかあったら面白いかも。
でも虚数乗の場合は２つかけて実数にするとか条件が付きそうだけど。