フラクタル画像集（その６）

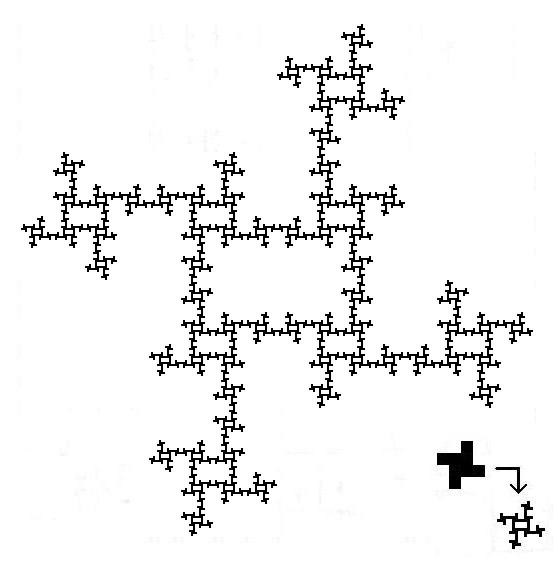
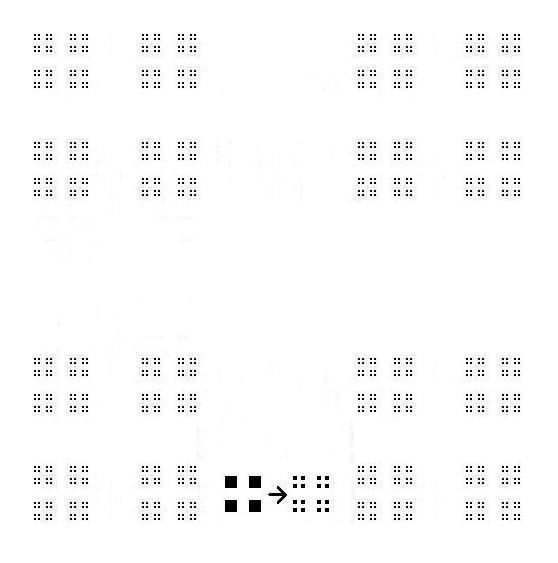
　Log４－１０≒１．６６次元↓





　逆に配列した。次元数は同じ↓





　これも同じ次元数だ↓





　向きを逆に並べた↓





　Log４－１１≒１．７２９７次元↓





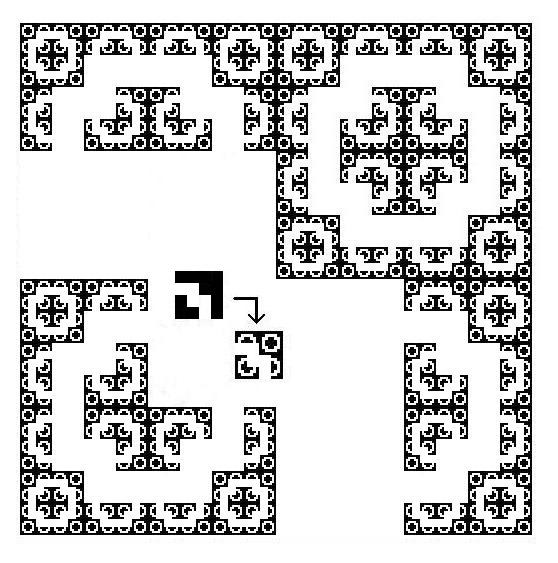
　逆に並べた。次元数は同じ↓





　Log４－１２≒１．７９２４８次元↓





　逆に並べた↓





Log４－１０≒１．６６次元↓





　並べ方を変えた↓





　Log４－１２≒１．７９２４８次元↓





　逆向きに並べた↓

フラクタル画像集（その５）

　Log４－１０≒１．６６次元↓





　配列を逆にした↓





　上のと同じ次元数↓





　配列を逆にした↓





　最初から向きはすべて同じ。Log４－８＝１．５次元↓


　


　それぞれの向きを変えた↓





　上のと逆方向に並べた↓





　次元数は同じで、配置が異なる。向きはすべて同じ↓


　


　それぞれの向きを変えた↓





　逆方向に並べた↓





　（その４）の一番下の図を、それぞれの向きを変えて並べた↓





　向きを逆にした↓


　　

フラクタル画像集（その４）

　「底」が４のフラクタル画像の続き。
　Log４－８＝１．５次元





　配列の仕方を変えた↓





　右上から左下に向けての消去を繰り返した。Log４－１２≒１．７９２４８次元↓





　配列の仕方を変えた。その１↓





　その２↓





　Log４－８＝１．５次元↓





　鈎爪のような恰好を組み合わせた。Log４－９≒1.5849625次元↓





　逆方向にそれぞれを並べてみた↓




　Log４－１０≒１．６６次元↓





　それぞれを逆に並べた↓





　最初から並べる向きがすべて同じ↓





　上と次元数は同じ↓

フラクタル画像集（その３）

　右下のＬ字状の３個の消去の繰り返しの図。シルピンスキーの変形版だ↓





　右下のほうの２つの消去の繰り返し↓





　右下と左上をＬ字型に残して、この後の配列の仕方を変えて、左下から右上にかけての消去を繰り返した↓








　これに真中を埋めた図を作り、その後の配列を変えてみた↓







　今度は、底が４のフラクタル図形を作成してみた。第二カントール集合から↓





　これを縦方向に１次元状態に引き伸ばした。縦成分として１が追加され、０．５＋１＝１．５次元となる。正方形を縦４×横４＝１６分割して特定の箇所を消去し、同じ操作を繰り返していく。





　縦方向と横方向共に第二カントール集合状態の図を作成した。０．５＋０．５＝１次元になる。log４－４＝１





　×印状の図形を繰り返した。Log４－８＝１．５次元





　唇の恰好を斜状にした図を繰り返した。Log４－１２≒１．７９２４８次元





　配列の仕方を変えてみた↓




　　
　さっきの図から隅を消去して繰り返した。Log４－１０≒１．６６次元

フラクタル画像集（その２）

　正方形を、縦２×横２＝４分割して右下の１個を消去し、残った３個の正方形に同様の操作をして以降同じことを繰り返していく。この方法でフラクタルを作成すると、意外なことに直角二等辺三角形版のシルピンスキーのギャスケットが出来上がった。最初どんな図形ができるのか予想してなかったが、この方法でも同図形が出来上がるとは予想外だった。log2-3≒１．５８４９・・・・次元となり、図を見れば分かるように、一辺の長さが２倍になると、この「亜面積」は３倍になる。





　ついでに、同じ方法で作成した図を貼り付ける。これは、消去した箇所を次の正方形の中心部に向けて配置することを繰り返してできた図である。次元数は同じで、やはり一辺を２倍にすると亜面積は３倍になる。　





　今度は逆に、空白部を外側に並べて作成してみた。次元数は同じ↓


　


　今度は、正方形を縦３×横３＝９個に分割した、「底」が３のフラクタル図形を作成してみた。
　底が３のフラクタルとしては、カントール集合がある。最初正方形から出発してこの図形を作成することも可能だ。





　このカントール集合を、縦方向に１次元状態に引き伸ばすとカントール集合の２次元版、というか、カントール集合に縦方向の１次元成分を加えたフラクタル図形になる↓





　これはlog3-6≒1.63092975次元になる。カントール集合はlog3-2≒0.63092975次元であり、これに縦方向の１次元を足すと、1.63092975・・になり、一致する。
　こんどは、縦方向もカントール集合状態の図を作成してみる↓





　これは、log3-4≒1.2618595・・次元になる。横の次元数成分のlog3-2≒0.63092975・・に縦の次元数のlog3-2≒0.63092975・・を加算すると、1.2618595・・であり、やはり一致する。

　次は×状に残してあとは消去した図である。これはlog3-5≒1.46497352次元であり、長さが３倍になると亜面積は５倍になる。さっきの図の次元数がコッホ曲線と同じなのに似ていないが、こちらはいくらか似ている↓




　白黒を逆にすると、黒の突起部が第二コッホ曲線の凸部に似て見える↓






　さっきのシルピンスキーのギャスケットのように、右下側部の４個を消去することを繰り返すとこういうのが出来上がった。いくらか似ている。log3-5≒1.4649735次元





　この図に最右下部を加えて同じ操作を繰り返した。





　今度は「凸」型から出発した図だ。コッホ曲線と同次元だが、全然似ていない↓



　図のように、Ｌ字状のを対に配置し、残りを消去することを繰り返した。間隙部がコッホ曲線の六角形の雪印模様を歪めたような恰好の図になった。log3-6≒1.63092975次元




　上図の中心部を埋めて作成した↓