相対性理論 最後の証明 重力波 「197」「215」

相対性理論　最後の証明　重力波  

 科学　索引　1goodシネマ　索引

 重力波（じゅうりょくは、英語: gravitational wave）は、一般相対性理論において予言される波動であり、

時空（重力場）の曲率（ゆがみ）の時間変動が波動として光速で伝播する現象である。

２０１４年春、岐阜県飛騨市の池ノ山地下深くに、長さ６キロの巨大なL字型トンネルが姿を現した。

ここで２０１５年１２月から観測を始めるのが、東京大学宇宙線研究所を中心に国内外６０以上の機関が参加し１５０億円の予算を投入する大型プロジェクト、

最先端の大型重力波望遠鏡「KAGRA（かぐら）」だ。今、各国の研究機関が 世界各地に巨大な観測装置を建設し、重力波観測の一番乗りを目指している。

重力波とは、物理学者アルバート・アインシュタインが、およそ100年前に一般相対性理論のなかで予言した現象だ。

アインシュタインは、質量を持つ天体は周囲の空間を歪め、その歪みは波のように光の速さで伝搬すると考えた。

宇宙を海とイメージすれば、天体という船が動くたびに、波のように重力波が生まれ宇宙を伝わっていくというものだ。

宇宙で生まれる無数の重力波は地球に届くと、人間の耳で聞こえる周波数帯であるため、もし増幅することができれば"宇宙 のささやき"が聞こえるという。

しかし、重力波はあまりに微弱で検出困難なため、多くの科学者の直接観測の試みは失敗に終わり、「アインシュタイン最後の宿題」と呼ばれてきた。

重力波は、質量を持つ全ての物質が運動する時に発生し、透過性が高いという特徴を持っている。

その 特徴を利用すれば、全く新しい天文学の観測手段を手に入れられると期待されている。

例えば、従来の電磁波を使った望遠鏡では観測できなかったブラックホール誕生の瞬間や中性子星と呼ばれる重い星同士の衝突など、姿は見えないが強い重力を持つ天体現象を捉えることができるようになる。

アインシュタインの最後の宿題"重力波"を解明しようとする科学者たちの100年の挑戦。

そして重力波によって新たな宇宙の姿を捉えようとする重力波天文学の誕生に迫る。

E = mc²（イー・イコール・エム・シーじじょう、イー・イコール・エム・シー・スクエアド）とは、

エネルギー (E) = 質量 (m) × 光速度 (c) の 2 乗

一般相対性理論によれば、大質量の物体は周囲の時空を歪ませる。すなわち、重力とは時空の歪みであるとして説明される。

その理論的な帰結・骨子となるのが、次のように表されるアインシュタイン方程式である。

左辺は時空がどのように曲がっているのか（時空の曲率）を表す幾何学量であり、右辺は物質場の分布を表す量である。

おおざっぱに言えば、星のような物質またはエネルギーを右辺に代入すれば、その物質の周りの時空がどういう風に曲がっているかを読みとることができる式である。

空間の歪みが決まれば、その空間中を運動する物質の運動方程式（測地線方程式）が決まるので、物質分布も変動することになる。

左辺の  はアインシュタイン・テンソルと呼ばれる。  は宇宙定数であり、この項は宇宙項と呼ばれる。

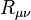  はリッチテンソル、 はスカラー曲率である。どちらも時空の計量テンソル  の微分で書かれる幾何学量である。 つまりアインシュタイン方程式は計量についての連立偏微分方程式の形をしている。

右辺の 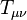 はエネルギー・運動量テンソルである。 係数  はアインシュタインの重力定数と呼ばれ、 ニュートンの重力定数 G と  の関係にある。（π は円周率、c は光速度）

アインシュタイン方程式はテンソルの方程式であり、時空の添字 μ,ν はそれぞれに時間1次元と空間3次元の4成分を動き 10 本の方程式を与える。

このうち、4本はエネルギー保存則と運動量保存則に対応するものであり、 の空間成分に関係する残りの6本の方程式が時空の運動方程式に相当する。

これらは時間微分2階の偏微分方程式6本（あるいは時間微分1階の偏微分方程式12本）であるが、座標の選択の自由度（ゲージの自由度）が4つ、保存則を満たしながら時間発展を行うための拘束条件が4つあると考えれば、

たとえ真空中であっても1階の微分方程式4本（2階に直せば2本）の自由度が残る。この自由度は時空の歪みを周囲に波として伝える「重力波」のモードが2つあることを意味している。