α上位とα下位の壁（偏差値60オーバーのせめぎあい）

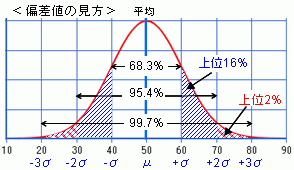
小学生の時、よく理解できなかった偏差値ですが、
要は母数や難易度の異なる試験条件においても、
点数と人数の度数分布を正規分布に当てはめることで、
点数を比較的確からしい順位へ変換することのできる、
統計的手法です。
ただし、受験者と点数の度数分布が正規分布をしていることが
前提。

サピαクラス（３クラスある校）の偏差値ですが
α３：59～63
α２：63～67
α１：67～
くらいの割り振りでしょうか。

この偏差値を前提に考えると、
α３：標準問題ミスなく確実にとれてちょっとした応用問題も解ける
α２：ちょっとした応用問題はもちろん、調子がよいときは難関校の受験問題も解ける
α１：難関校の問題もどんどん解ける
なイメージですかね。

で、このα３（偏差値60辺りをいったりきたり）とその先の間には
ちょっとした隔たりがあると思います。

ちょっと賢い、要領のいい子はα３にすぐに到達します。
要領の悪い子でも、親がしっかりとサポートしてミスを修正していけば
到達できると思います。

でも、その先に、α上位クラスには行くには、文字通りプラス”α（アルファ）”が必要になってくるのです。

そのプラス”α”とは、「○○算では解けない領域」です。


中学入試の算数にはいろんな○○算があります。
つるかめ算、旅人算、植木算、……
子供は問題を見た瞬間、どの○○算を当てはめるのかを考えます。
ませた子供は未知数をx,yとおいて連立方程式で解こうとします。
実際、大半の○○算はそれで解けてしまいます。

ですが、63オーバーの難関校の問題は○○算では解けません。
連立方程式でも解けません。（未知数が方程式の数よりも多いからです）

難関校の問題は制約と規則性に気をつけて、全てを列挙する

が標準的な解答法です。

このゲームチェインジに気づけること、慣れること、
○○算が使えないことを恐れないこと……。
それが分水嶺になります。

応用問題といいますが、応用というよりは別物だと思います。
むしろ○○算の知識が邪魔なんじゃと思うくらい……
（実際にはそんなことはないんですが）

30年前、それらの問題を見たとき自分も思いましたね。
これって、（○○算とかやってきた）今までの勉強って意味なくね？
と。


本当に頭のいい子（地頭70オーバー）はこの辺を感覚でクリアするから、
世の中、平等とはいかないものです。。。