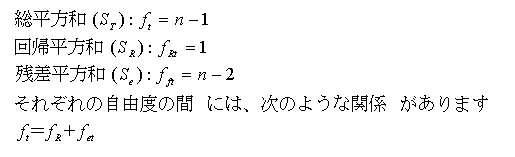前回は、回帰直線がデータを説明できる程度を学びました。今回は、回帰直線がデータを説明できなかった誤差、つまり残差に存在する変動を学びます。
ところで、今まで、データを回帰直線で表すことを考えました。これを、回帰モデルと呼びます。回帰モデルでは、誤差εを、標準偏差σであらわしておきました。ここで、前回、残差の計算方法を学んだことを思い返しましょう。すると、この計算方法を用いれば、残差の変動、つまり残差分散を計算できることが分かります。そして、いまデータは、サンプリングされた結果です。従って、残差分散が、母集団の値に対して偏りがないないように調整する値が必要です。このように、母集団の値に対して、偏りがないように調整された推定値のことを、一般的に、不偏推定量と呼びます。その意味で、不偏推定量は、母集団と標本との間をつなぐ、とても重要な値といえます。
では、さっそく、残差分散を求めてみましょう

この残差は、標本からのものですから、残差分散の不偏推定量を考える必要があります

最後に、各種平方和の自由度を、以下に示しておきます
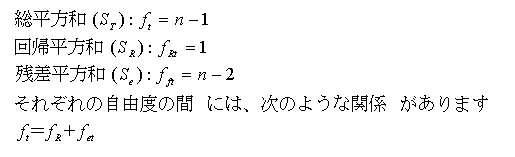
ところで、今まで、データを回帰直線で表すことを考えました。これを、回帰モデルと呼びます。回帰モデルでは、誤差εを、標準偏差σであらわしておきました。ここで、前回、残差の計算方法を学んだことを思い返しましょう。すると、この計算方法を用いれば、残差の変動、つまり残差分散を計算できることが分かります。そして、いまデータは、サンプリングされた結果です。従って、残差分散が、母集団の値に対して偏りがないないように調整する値が必要です。このように、母集団の値に対して、偏りがないように調整された推定値のことを、一般的に、不偏推定量と呼びます。その意味で、不偏推定量は、母集団と標本との間をつなぐ、とても重要な値といえます。
では、さっそく、残差分散を求めてみましょう

この残差は、標本からのものですから、残差分散の不偏推定量を考える必要があります

最後に、各種平方和の自由度を、以下に示しておきます