復習 それぞれの数字の差を取って、でてきた2つの整数の最大公約数を求める

 

では、「本当に理解する」とはどういうことなのか、
問題を使って具体的に示していきます。

問題：82、121、186の3つの数字をある整数で割ったら、同じ余りがでました。
どんな数で割ったのでしょうか。また、余りはいくつですか。

解き方を知っていると、
それぞれの数字の差を取って、でてきた2つの整数の最大公約数を求める
ということで、パッと答えを出すことができます。
ただ、やはり、何で、まず差をとるのか
なぜその差の最大公約数で答えが求められるのか

ここをしっかりと答えられるか、お子様にも質問してみてください。

【解説】
式での解説：
121-82＝39
186－121＝65

39と65の最大公約数は13
13の約数＝1，13のみ
1ではない整数は13のみ。よって、割った数は、13
また、余りは、82÷13＝6…4
121÷13＝9…4
186÷13＝14…4　となりますので、
余りは、４

式は以上のようになりますが、これでは、まだ、本当にわかっているのかが不透明です。

それでは、もう少し詳しく見ていきましょう。

問題で言われることを線分図で表してみると、

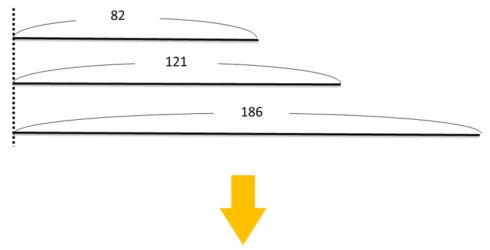
この3つの整数は何かで割って余りが同じ整数になったので、
余りの部分を線分図の一番左（緑色の部分）に取ります。
そうすると、それ以外の部分は、必ず何かで割れるわけなので、
121と82の差
186と121の差
の部分も、必ず割る数（青い部分）で割ることができます。

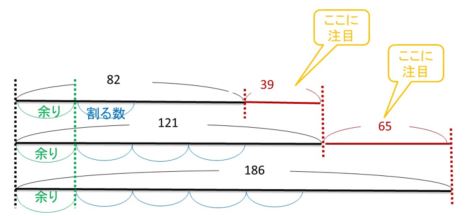
だから、121-82=39と186-121＝65という数字がでてくるのです。

「なぜ差を求めるのか」

という理由がこの図で示されています。

ここの部分をしっかりと言葉で説明できるか、図を描くことができるか、
こういった部分を、もしご家庭で確認できればやっていただいた方がいいと思います。

問題を解く上での「視点」がどこにいくのか、ということが、意外とどの問題でも大切です。
どこに目を向けて解くのか、それを習得していってほしいと思っています。

82-余り、121-余り、186-余りと言われても、まだそれだけでは具体的な数字がでてきません。
だから、問題が解けないということになってしまいます。

そうではなくて、差の部分が割れる数でなくてはいけないということに、気付けるかどうかということに
なります。

式だけ覚えておしまい、この問題は解けたと錯覚してしまう生徒さんを多く見ています。
なかなか、一つ一つを問いかけながら問題を解くということは、時間的にも難しいかもしれません。
また、どういう問いかけが、その問題の本質を説いているのかは、やはりプロにお任せいただいた方が
いいでしょう。