直前期に平面図形の知識 ヒポクラテスの三日月 大日本はひとつの家族

今回のお題は
「直前期に平面図形の知識をチェック！」

いわゆる「公式」の確認ではありません。

知っていればあっさり解ける

そんな図形知識について
さくっと目を通して確認してください。

この時期の6年生にとって
無駄な時間を過ごす余裕はないので
手短かにいきます。

本日のブログは全部で3題
知っている人なら所要時間 10秒×3題＝30秒 です。

5年生以下のお子さんにとっても
豆知識として頭に入れておいて損はありません。

では、いきましょう。

　ひたすら時短です　

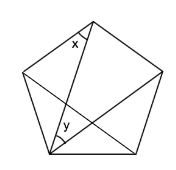
【問1】
次の正五角形において
角x、角yの大きさはそれぞれ何度ですか。

≪解説≫
正五角形の中にひいてある直線が対角線だけのとき
正五角形の内部には
①36度
②36度×2＝72度
③36度×3＝108度
の3種類の角度しか存在しません。

図がある程度正確であれば、見た目だけで判断できます。

細ければ36度
直角より少し小さければ72度
直角より少し大きければ108度

ということで
角x、角y
ともに36度です。

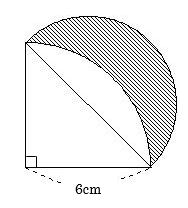
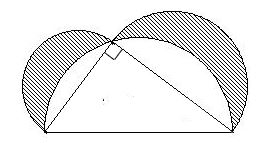
【問題2】
次の図形は、直角二等辺三角形、四分円、半円を組み合わせた図形です。
斜線部分の面積は何㎠ですか。

≪解説≫
みなさんご存知の「ヒポクラテスの三日月」です。

2つの三日月（斜線部分）の面積の合計は直角三角形の面積と等しい
というものですね。

この直角三角形が「直角二等辺三角形」のとき
2つの三日月は同じ大きさになります。
それを半分にしたものが
さきほどの図形の正体です。

ということで、答えは
6×6÷2＝18㎠　　です。

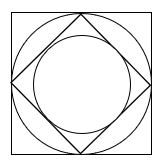
【問題3】
次の図形は大小2つの正方形と大小2つの円を組み合わせた図形です。
2つの円の中心は同じで、大きい円は大きい正方形の内側に
小さい円は小さい正方形の内側に、どちらもぴったりと接しています。
また、小さい正方形の頂点は、すべて大きい円の円周上にあります。
このとき、大きい円の面積は小さい円の面積の何倍ですか。

≪解説≫
大きい正方形の各辺の中点（真ん中の点）を結んでできたのが
小さい正方形。
よって、大きい正方形の面積は小さい正方形の面積の2倍です。

ここで
大きい円は大きい正方形の内側にぴったりと接していて
小さい円は小さい正方形の内側にぴったりと接している

ということは、大きい円も小さい円の2倍になります。

ちなみに
「大きい正方形から大きい円をひいた部分の面積」
も
「小さい正方形から小さい円をひいた部分の面積」
の2倍です。

“加比の理”と呼ばれる考え方ですね。

　結局、ラクするのがいちばん　

中学受験の算数においては
上記のように
見てすぐ答えが出せる問題というものがあります。

知っていれば得する
知っていればラクできる

そんな知識は最後まで大切に
頭の中に入れておいてください。

おしまい。

それでは、また～