てんびん図をつかいこなす 男は家を守る

10％の食塩水100ｇに、濃度がわからない食塩水Ａを50ｇ加えて、さらに50ｇの水を加えたところ、食塩水の濃度は６％になりました。加えた食塩水Ａの濃度は何％ですか。
(海城中　平成二十七年　第１回)

この問題の場合、公式で解くという人も多いでしょう。
私も本番のテストとなれば、以下の式で、解くかもしれません。

食塩水Ａの食塩の重さ＝(100＋50＋50)ｇ×－100ｇ×＝２ｇ
食塩水Ａの濃度＝２ｇ÷50ｇ＝0.04　→　４％

ですが、本日、お伝えしたいのは、武器(解法)の使い方なので、
別の方法で、解きます。

算数の食塩水といえば、公式以外に、てんびん図が解法としてあります。

そして、てんびん図は、理科でのてこのつりあいを利用しています。
てんびん図とてこのつりあいをまとめると、次のような感じですね。

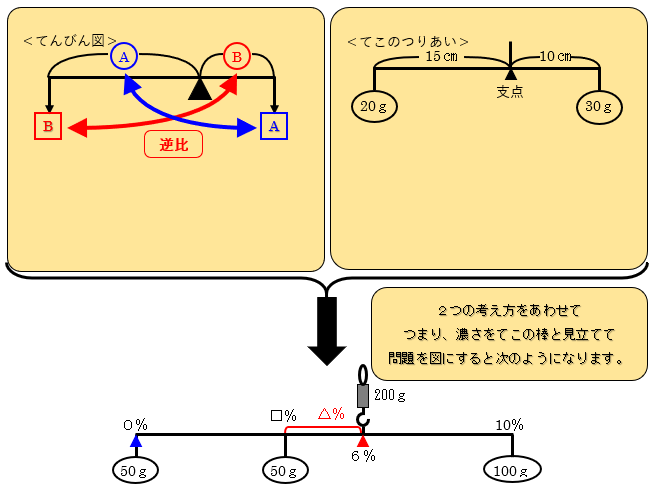
上の図、そして、つりあっているときは支点をどこでもよいことを使って、問題を解くと、

解法①　０％を支点とする
左に回すはたらき＝200ｇ×６％
右に回すはたらき＝50ｇ×□％＋100ｇ×10％
□＝４％

解法②　６％を支点とする
左に回すはたらき＝50ｇ×６％＋50ｇ×△％
右に回すはたらき＝100ｇ×(10－６)％
△＝２％　　□＝６－２＝４％

となります。理科の知識が算数でも使えることが体感できましたか？
めんどくさい…公式で解けるからいいのでは？と思う人もいるかもしれませんが、
１つの解法しか知らないと、発展問題に太刀打ちできないことがあります。
ですから、さまざまな武器(解法)を根本原理まで理解し、その武器を磨くのです。

では、実際にこの武器を発展問題で使ってみましょう。

次の問題です。

400ｇずつ食塩水が入っている容器Ａ、Ｂ、Ｃがあり、容器Ｃの食塩水の濃さは３%です。容器ＡとＢからそれぞれ200ｇずつ取り出して混ぜると３%の食塩水になりました。次に、容器Ｃから200ｇずつとりだして容器Ａ、Ｂに入れると容器Ａの食塩水の濃さは容器Ｂの食塩水の濃さの２倍になりました。はじめの容器Ａの濃さを求めなさい。

この問題を公式で解こうとすると、結構時間がかかると思います。

ということで、先ほどの、てんびん図とてこのつりあいという武器を使います。

この問題のポイントは、すべて200ｇずつの食塩水を混ぜていること、
解法のポイントは、濃さの数値をてこの棒と見立てているので、０％から棒をかいてみることです。

では、混ぜているようすをでんびん図にしてみましょう。

・容器ＡとＢからそれぞれ200ｇずつ取り出して混ぜると３%の食塩水になりました。

＜図１＞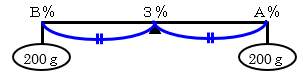

 

・容器Ｃから200ｇずつとりだして容器Ａ、Ｂに入れると容器Ａの食塩水の濃さは容器Ｂの食塩水の濃さの２倍になりました。

＜図２＞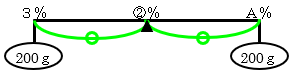

＜図３＞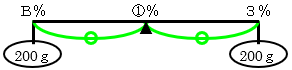

 

ここで、技をひとつ。
図１から図3のてんびん図をひとつにまとめてみましょう。
ひとつにまとめると、次のようになります。

 

図１の１つ分の長さと、図２、３の２つ分の長さが同じです。

そして、１つにまとめたことにより、

図から、３つ分が３％となり、５つ分のＡ％は５％となります。

ほぼほぼ計算せずに解答できました。

このように、根本原理を正しく理解し、使うことによって、さまざまな問題が解けますので、
１つの問題に対して、１つの解法を暗記するのではなく、
解法の原理を理解していきましょう。

他にも、てんびん図は、算数では平均の問題でも使えますし、理科ではカロリー計算にも使えます。