身体均整募集中!http://www.kinsei-gakuen.com/
内臓調整療法師会 http://kinsei.main.jp/naizoutyousei/
眠りとお通じの整体院 http://kinsei-gakuen.com/kansaikinseiin/
やすらぎ創健堂のhpのデザインが大きく変わりました。トップページから入ってごらんください。リンクを張っていただける方は、ご協力をお願いします。
前回はユークリッド幾何学の入り口のお話のところで途切れてしまいました。少し立ち入った話になっていますが、手技療法の対極にある「実証科学における客観性」について考えるなかで、とくに数学の役割を理解する一つの手かがとして、クラインのエルランゲン・プログラムについて考えようということでした。
変換群とはなにか?
ウィキペディアの「エルランゲン・プログラム」の記述を引用すると、
クラインはこの中で、幾何学を集合に対する変換群の作用によって分類し、その中で出てくる不変量(不変式)を扱うものだと定義した。例えばユークリッド幾何は合同変換で変わらない性質を扱う分野であり、射影幾何は射影変換で変わらない性質を扱う分野だ、というのである。
とあります。
「集合に対する」「不変量(不変式)を扱う」云々のところは、とりあえず置いておいて、「変換群」というものがエルランゲン・プログラムを考える鍵になっていることがわかります。
変換群という言葉だけを聞くとものものしいですが、実際に図で見るとたいしたことではありません。
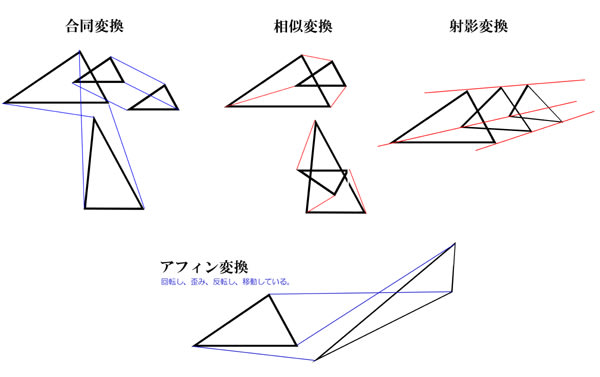
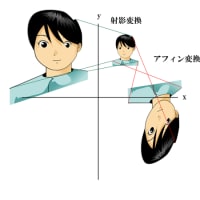
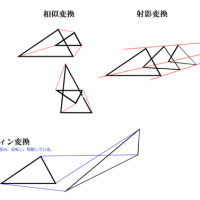
ここに挙げた、合同変換、相似変換、射影変換、アフィン変換などが「変換」という行為の具体的な姿です。これらをまとめて「変換群」といっているのです(※実際には、もう一つ「複素変換」という変換のタイプがあります。これについては次回に紹介します)。
クラインはこの変換群の考え方を使って、非ユークリッド幾何学を統合してみせたのです。
そもそもユークリッド幾何学は定規とコンパスの幾何学です。上にあげたよう変換を自由に行うことはできませんでした。
ただ、長さはコンパスを使えば同じものを自由に作り出すことができます。角度は平行線を使えば同じものを作り出すことができます。図形の角度や大きさを自由に変えることはできませんが、合同変換は自由におこなえます。
つまり長さと角度が「不変量」として保存される幾何学と定義することができます。
変換群のアルゴリズム
ユークリッドの時代には、図形を移動したりひっくり返すという作業が、数学的な厳密さに欠けると考えられていました。
ゼノンのパラドクスによれば、ある物体が落下するためには、かならず地面と間の中点をとおらねばならず、次にその中点と地面との中点をとおらねばならず、さらにその中点と地面との中点をとらねばならないから、実際、落下しているように見えて、地面に到着することはない、そのような疑いがあると考えられていたのです。
しかし、解析幾何学が生まれ、時代は一変しました。変換という行為は、座標系のなかの関数としてごく当たり前に考えられるようになったのです。
たとえばコンピュータ・ゲームや映画のコンピュータグラフィックスなどでは、複雑な図の変換が縦横無尽に繰り広げられていますよね。図形の変換は、わたしたちの日常生活になじみ深いものになっているのです。
現在の高校数学で非ユークリッド幾何学が取り扱われるのも、そのような点から考えると理解できます。変換には行列の知識が必要ですが、知りたい人は自分で専門的に勉強してくださいということでカリキュラムから削られています。学ぶ順序からすると、いきなり行列を学ぶより親切だと思います。
ここでは少し行列の話をします。変換群の性質は、そのアルゴリズムによって明解に定義できるからです。少しお付き合いください。
さて、変換とは座標上の点(x、y)を別の点に移動する関数です。大雑把に次のように表現できます。

この関数は行列式で表すと以下のように一般化して表すことができます。

並行移動する合同変換では、x方向に+3、y方向に+5のように移動すればよいわけですが、この場合は、以下のように行列の和としてあらわすことができます。

このとき先頭についている

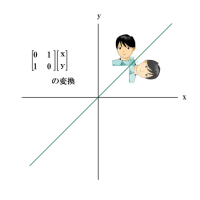
は単位行列と呼ばれるもので、x、yの値を変化させない関数です。これを次のようなひっくり返った形にすると

xがyの値に、yがxの値に変換されます。

つまり原点を通って45°で右肩上がりの直線上の点、つまりx=y上の点は動かないが、それ以外の点はこの線を境に対称に変換された合同変換の図形になります。
図形の回転とアフィン変換
回転させるためには三角関数を使ってあらわします。角度θの回転では、以下のようになります。

三角関数は、角度をベクトル(内積)に変換するものです。具体的な長さ(a、b)式で表すと
 、
、 
になります。ヒルベルト『幾何学基礎論』では、このように式による表現が採用されています。(x、y)が次のような(x'、y')に変換されます。
 、
、 
先に申し上げたように、変換という作業は以下の行列式として一般化できます。

このとき変数 a、b、c、d の値によってxやyが2倍になったり3倍になったり、x、yが入れ替わったりといった変換が起こります。x、yが同じ割合で変化すれば相似変換になります。
並行移動したり、入れ替わったり、回転するだけなら合同変換です。
a、b、c、d の違いによって、変換のなかにいくつかのタイプ(群)が存在することが実感していただけると思います。
つまり「変換群」は、このa、b、c、d の取り方によって決まるのです。アフィン変換はクラインの時代にはまた考えられていませんでしたが、これと少し違った形になります。

いずれにしても、このように行列式のアルゴリズムで見ると図の変換がうまく整理できます。
このアルゴリズムをプログラムに反映させると、図形の変換プログラムになります。そういったプログラムの書き方についてもネット上では様々な情報が紹介されています。
一見するととても難しく感じます。これはちょうどマイクロソフトのosがMS‐DOSだった時代、タックシール一つ打ち出すにも、英語のコマンド打ち込まなければならなかった状態とにています。
実際の図の姿になると抵抗感がなくなります。web上、グラフィック上では、こういった変換がさまざまなところでおこなわれています。
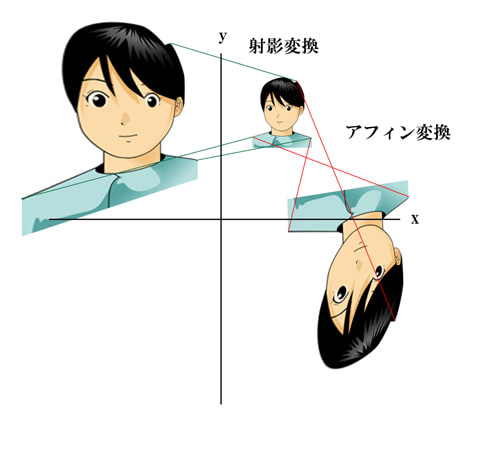
ここには数学の役割の変化があります。18世紀末から起こった形式主義による数学の現代化は、このさきがけだったのです。
「変換群」で非ユークリッド幾何学がどのように統合されるのか?
非ユークリッド幾何学は1860年ころを契機に、ガウス、ボヤイ、ロバチェフスキー、リーマンなどの発案になるものが次々と世に知られるようになっていきました。契機になったのは1855年のガウスの死でした。
死後公開されたガウスの遺稿で、大数学者ガウスが非ユークリッド幾何学の存在をよく理解していたことが明らかになったのです。
ガウスの考案した非ユークリッド幾何学は、平行線が2本引けるというものです。
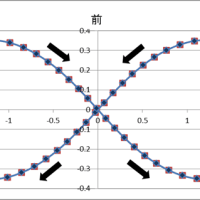
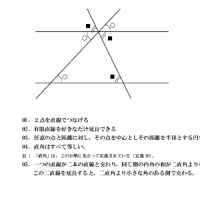
これは大平原の駅のホームに立ってどこまでも続くまっすぐな線路を見ている姿を想像するとことからはじまります。
平行な2本のレールが上り方向と下り方向、それぞれに地平線に向けて収束していきます。一本のレールの上から見ると、上り方面に収束する一本と、下り方面に収束する一本、それぞれ2つの平行線が見えます。これあ1点透視図の世界です。
地平線は無限遠点として除外して考えると、ある直線外の一点を通る平行線が2本引けることになります。
このように考えても、一定の制約のなかで幾何学がなりつことをガウスは理解ました。しかし、そのことを発表しませんでした。神学論争のような手の負えない議論に巻き込まれるのを恐れたのではないかと考えられています。
ガウスの考えた非ユークリッド幾何学は、変換群の観点から見ると、ユークリッド幾何学を射影変換した幾何学といえます。
つまり、とてもきれいに整理することができるのです。エルランゲン・プログラムの卓見です。
リーマンの幾何学とポアンカレ円盤
しかし、この方法が非ユークリッド幾何学を統合する唯一の方法というわけではありません。
リーマンの非ユークリッド幾何学は、楕円幾何学、放物線幾何学、双曲線幾何学など、球面の曲げ率を多様に変化させるものでした。
このような視点に立つとユークリッド空間は、曲げ率0の空間の幾何学ということになります。この方法でもきれいに統合できるのです。
ポアンカレ円盤は、このような非ユークリッド幾何学を見渡す別の見方です。
このような19世紀末の非ユークリッド幾何学をめぐる議論に触れると、勃興しつつある現代数学の息吹を感ずることができます。
このような数学は、実証科学の理論構築になくてはならないものとなっていきます。マクスウェルの波動方程式しかり、ボルツマンの熱平衡力学しかり、アインシュタインの相対性理論しかりです。
数学は地上の束縛を離れて、公理系という仮想空間のなかで爆発的に発展を遂げてゆくことになります。これこそが、数学の形式化であり、今日の「客観性」に張り付いている重要な側面なのです。
次回は、このあたりのことから考えてみたいと思います。
(つづく)