正方形を、縦2×横2=4分割して右下の1個を消去し、残った3個の正方形に同様の操作をして以降同じことを繰り返していく。この方法でフラクタルを作成すると、意外なことに直角二等辺三角形版のシルピンスキーのギャスケットが出来上がった。最初どんな図形ができるのか予想してなかったが、この方法でも同図形が出来上がるとは予想外だった。log2-3≒1.5849・・・・次元となり、図を見れば分かるように、一辺の長さが2倍になると、この「亜面積」は3倍になる。

ついでに、同じ方法で作成した図を貼り付ける。これは、消去した箇所を次の正方形の中心部に向けて配置することを繰り返してできた図である。次元数は同じで、やはり一辺を2倍にすると亜面積は3倍になる。

今度は逆に、空白部を外側に並べて作成してみた。次元数は同じ↓

今度は、正方形を縦3×横3=9個に分割した、「底」が3のフラクタル図形を作成してみた。
底が3のフラクタルとしては、カントール集合がある。最初正方形から出発してこの図形を作成することも可能だ。

このカントール集合を、縦方向に1次元状態に引き伸ばすとカントール集合の2次元版、というか、カントール集合に縦方向の1次元成分を加えたフラクタル図形になる↓

これはlog3-6≒1.63092975次元になる。カントール集合はlog3-2≒0.63092975次元であり、これに縦方向の1次元を足すと、1.63092975・・になり、一致する。
こんどは、縦方向もカントール集合状態の図を作成してみる↓
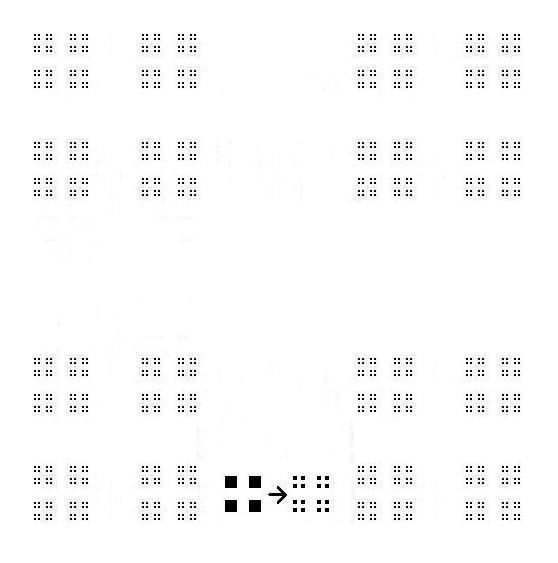
これは、log3-4≒1.2618595・・次元になる。横の次元数成分のlog3-2≒0.63092975・・に縦の次元数のlog3-2≒0.63092975・・を加算すると、1.2618595・・であり、やはり一致する。
次は×状に残してあとは消去した図である。これはlog3-5≒1.46497352次元であり、長さが3倍になると亜面積は5倍になる。さっきの図の次元数がコッホ曲線と同じなのに似ていないが、こちらはいくらか似ている↓

白黒を逆にすると、黒の突起部が第二コッホ曲線の凸部に似て見える↓

さっきのシルピンスキーのギャスケットのように、右下側部の4個を消去することを繰り返すとこういうのが出来上がった。いくらか似ている。log3-5≒1.4649735次元

この図に最右下部を加えて同じ操作を繰り返した。

今度は「凸」型から出発した図だ。コッホ曲線と同次元だが、全然似ていない↓

図のように、L字状のを対に配置し、残りを消去することを繰り返した。間隙部がコッホ曲線の六角形の雪印模様を歪めたような恰好の図になった。log3-6≒1.63092975次元

上図の中心部を埋めて作成した↓


ついでに、同じ方法で作成した図を貼り付ける。これは、消去した箇所を次の正方形の中心部に向けて配置することを繰り返してできた図である。次元数は同じで、やはり一辺を2倍にすると亜面積は3倍になる。

今度は逆に、空白部を外側に並べて作成してみた。次元数は同じ↓

今度は、正方形を縦3×横3=9個に分割した、「底」が3のフラクタル図形を作成してみた。
底が3のフラクタルとしては、カントール集合がある。最初正方形から出発してこの図形を作成することも可能だ。

このカントール集合を、縦方向に1次元状態に引き伸ばすとカントール集合の2次元版、というか、カントール集合に縦方向の1次元成分を加えたフラクタル図形になる↓

これはlog3-6≒1.63092975次元になる。カントール集合はlog3-2≒0.63092975次元であり、これに縦方向の1次元を足すと、1.63092975・・になり、一致する。
こんどは、縦方向もカントール集合状態の図を作成してみる↓

これは、log3-4≒1.2618595・・次元になる。横の次元数成分のlog3-2≒0.63092975・・に縦の次元数のlog3-2≒0.63092975・・を加算すると、1.2618595・・であり、やはり一致する。
次は×状に残してあとは消去した図である。これはlog3-5≒1.46497352次元であり、長さが3倍になると亜面積は5倍になる。さっきの図の次元数がコッホ曲線と同じなのに似ていないが、こちらはいくらか似ている↓

白黒を逆にすると、黒の突起部が第二コッホ曲線の凸部に似て見える↓

さっきのシルピンスキーのギャスケットのように、右下側部の4個を消去することを繰り返すとこういうのが出来上がった。いくらか似ている。log3-5≒1.4649735次元

この図に最右下部を加えて同じ操作を繰り返した。

今度は「凸」型から出発した図だ。コッホ曲線と同次元だが、全然似ていない↓

図のように、L字状のを対に配置し、残りを消去することを繰り返した。間隙部がコッホ曲線の六角形の雪印模様を歪めたような恰好の図になった。log3-6≒1.63092975次元

上図の中心部を埋めて作成した↓




















