基本的な「山越え気流」の理論解析に用いられる古典的な解析モデルとして、このようなものが知られています。

ある高さH0[m]における等圧面を破線で表し、これを自由表面と呼びましょう。地表面付近の大気を、自由表面を境に上下2つの層に分ける二層構造で考えます。
そして、下層の温位をθ0[K]、上層の温位をθ0+Δθ[K]であるとします。そして、左側から速度U0[m/s]の風が流入するものと考えましょう。この時、U0が大きいほど(Frが大きいほど)流れは山を乗り越えやすく、風下では「おろし」と呼ばれる強風が発生しやすいことが理論的に明らかにされております。ここでFrとはフルード数の事です。
この「Fr数が大きい、小さい」というのは「実際の大気の状態とどのように対応するのか」を考えてみます。
フルード数Frが実数である時、すなわち「Fr∈R (※Rは実数全体の集合)」である時、根号(√)の中の数は正でなければなりません。つまり、「g(Δθ/θ0)H0>0」となります。
ここで、現実の問題を想定すると「U0>0 ∧ g>0 ∧ θ0>0 ∧ H0>0」となるので、Δθもまた「Δθ>0」となります。確かに、この解析モデルは、下層(θ0)よりも上層(θ0+Δθ)の温位が高い構造となっているため、安定成層「Δθ/Δz>0」となることが前提となっています。
つまり、安定性が増すとΔθは大きくなり、分母も大きくなるので、Fr数は小さくなる一方、安定性が減ると(不安定性が増すと)Δθは小さくなり、分母も小さくなるので、Fr数は大きくなる方向にシフトしようとします。
また、風速U0が増すと、分子も大きくなるので、Fr数は大きくなる一方、風速U0が減ると、、分子も小さくなるので、Fr数は小さくなります。
フルード数の式の形は大気安定性(分母)と風速(分子)のバランスを「一つの物差し」で表現していると言えるのです。これを簡単に描くと・・・
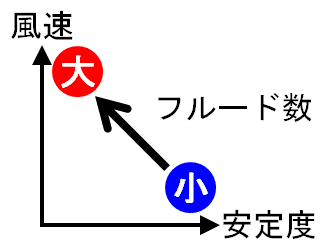
と言う事ですね。冬型の気圧配置の場合を考えると「上空の寒気が強まるにつれて、また季節風が強まるにつれてフルード数が大きくなる」という事です。
但し、大気安定性(分母)は(1/2)乗で効いて来るのに対し、風速(分子)は1乗で効いてくるので、風速に対する感度の方がより強いと言えるでしょう。風が強いとFr数が大きく、風が弱いとFr数が小さいと言えるのも、この辺の事情が絡んでいるようにも思えます。
ちなみに、工業熱力学や伝熱工学を学んだ方ならご存知のレイノルズ数(Re)やグラスホフ数(Gr)と、フルード数(Fr)の間には「1/Fr2 = Gr/Re2」という関係があります。この式を見ても風速に相当するレイノルズ数が2乗で効いているのに対し、グラスホフ数は1乗で効いていますね。なお、「1/Fr2」という形は、実際の方程式の中で適用されている形です。

ある高さH0[m]における等圧面を破線で表し、これを自由表面と呼びましょう。地表面付近の大気を、自由表面を境に上下2つの層に分ける二層構造で考えます。
そして、下層の温位をθ0[K]、上層の温位をθ0+Δθ[K]であるとします。そして、左側から速度U0[m/s]の風が流入するものと考えましょう。この時、U0が大きいほど(Frが大きいほど)流れは山を乗り越えやすく、風下では「おろし」と呼ばれる強風が発生しやすいことが理論的に明らかにされております。ここでFrとはフルード数の事です。
この「Fr数が大きい、小さい」というのは「実際の大気の状態とどのように対応するのか」を考えてみます。
フルード数Frが実数である時、すなわち「Fr∈R (※Rは実数全体の集合)」である時、根号(√)の中の数は正でなければなりません。つまり、「g(Δθ/θ0)H0>0」となります。
ここで、現実の問題を想定すると「U0>0 ∧ g>0 ∧ θ0>0 ∧ H0>0」となるので、Δθもまた「Δθ>0」となります。確かに、この解析モデルは、下層(θ0)よりも上層(θ0+Δθ)の温位が高い構造となっているため、安定成層「Δθ/Δz>0」となることが前提となっています。
つまり、安定性が増すとΔθは大きくなり、分母も大きくなるので、Fr数は小さくなる一方、安定性が減ると(不安定性が増すと)Δθは小さくなり、分母も小さくなるので、Fr数は大きくなる方向にシフトしようとします。
また、風速U0が増すと、分子も大きくなるので、Fr数は大きくなる一方、風速U0が減ると、、分子も小さくなるので、Fr数は小さくなります。
フルード数の式の形は大気安定性(分母)と風速(分子)のバランスを「一つの物差し」で表現していると言えるのです。これを簡単に描くと・・・

と言う事ですね。冬型の気圧配置の場合を考えると「上空の寒気が強まるにつれて、また季節風が強まるにつれてフルード数が大きくなる」という事です。
但し、大気安定性(分母)は(1/2)乗で効いて来るのに対し、風速(分子)は1乗で効いてくるので、風速に対する感度の方がより強いと言えるでしょう。風が強いとFr数が大きく、風が弱いとFr数が小さいと言えるのも、この辺の事情が絡んでいるようにも思えます。
ちなみに、工業熱力学や伝熱工学を学んだ方ならご存知のレイノルズ数(Re)やグラスホフ数(Gr)と、フルード数(Fr)の間には「1/Fr2 = Gr/Re2」という関係があります。この式を見ても風速に相当するレイノルズ数が2乗で効いているのに対し、グラスホフ数は1乗で効いていますね。なお、「1/Fr2」という形は、実際の方程式の中で適用されている形です。


















