物理 変数分離形 例題 (平成25年 数理科学・物理・地球科学 国家総合職過去問解説 多肢選択)

No95 まずrに対する重力加速度G(r)を求める。
天体のうちrより浅い部分のみが重力に寄与する。
その部分の体積は

質量は

位置rにおける質量mの物体にかかる重力は
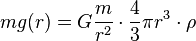
よって

よって文中の静水圧平行の微分方程式は
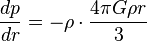
変数分離形なので、両辺drをかけて整理する
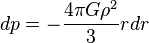
両辺積分する

条件r=a,p=0 を満たすように積分定数を調整して
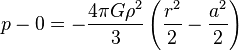
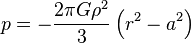
中心圧力p(0)は

解は1.
物理 変数分離形 例題 (平成25年 数理科学・物理・地球科学 国家総合職過去問解説 多肢選択)

No95 まずrに対する重力加速度G(r)を求める。
天体のうちrより浅い部分のみが重力に寄与する。
その部分の体積は

質量は

位置rにおける質量mの物体にかかる重力は
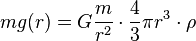
よって

よって文中の静水圧平行の微分方程式は
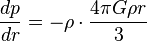
変数分離形なので、両辺drをかけて整理する
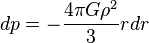
両辺積分する

条件r=a,p=0 を満たすように積分定数を調整して
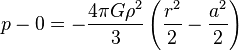
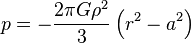
中心圧力p(0)は

解は1.
平成25年度 国家公務員試験過去問解答 一般職 電気電子情報 専門試験(多肢)No2 幾何
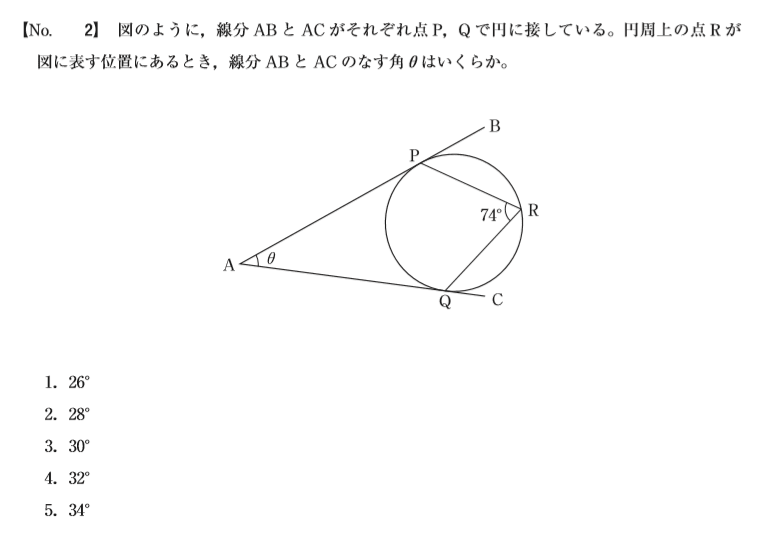

円の中心をOとします。
すると円周角の定理により
∠POQ=2×74=148°です。
また、P,Qが接点であることから、∠OPA=∠OQA=90°です。
四角形OQAPについて、内角の和は360°なので、
θ+90+148+90=360
方程式を解いて、
θ=32°
答え 4. 32°
平成25年度 国家公務員試験過去問解答 一般職 電気電子情報 専門試験(多肢)No1 複素数

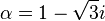 の偏角は
の偏角は
 ですので、
ですので、
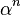 の偏角は
の偏角は  です。(ド・モアブルの定理) これがπの整数倍のとき、実数になりますので、nが3の倍数の時が答えです。
です。(ド・モアブルの定理) これがπの整数倍のとき、実数になりますので、nが3の倍数の時が答えです。
答え 2.n=3k
【2014年度 国家公務員試験総合職過去問解説 専門多肢選択式 数理科学・物理・地球科学 NO48 トートロジー】
P,Qを命題とするとき トートロジー(恒真式)は次のうちどれか。 ただし は命題X の否定を表すものとする
は命題X の否定を表すものとする

トートロジーを確認する手段のひとつに式がFALSEであると仮定して矛盾を導くというものがあります。
まず1. についてはPQ両方にFALSEを割り当てれば
についてはPQ両方にFALSEを割り当てれば
式がFALSEになるのがあきらかです。
2. 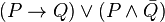 について、
について、
式がfalseとなるためには の左右が両方FALSEとなる必要があります。
の左右が両方FALSEとなる必要があります。
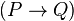 がFALSEになるのはPがTRUEでQがFALSEのときのみです。
がFALSEになるのはPがTRUEでQがFALSEのときのみです。
そのとき はTRUE[になります。これは前述の
はTRUE[になります。これは前述の
「 の左右が両方FALSEとなる」に矛盾しますので、これがトートロジーです。
の左右が両方FALSEとなる」に矛盾しますので、これがトートロジーです。
答え。2.
考え方のコツとしては、 で結ばれた式のほうがトートロジーになりやすいでしょうからこの問題の場合1.2.3.からチェックするといいでしょう。
で結ばれた式のほうがトートロジーになりやすいでしょうからこの問題の場合1.2.3.からチェックするといいでしょう。
また。4.はPとQが同値であるという主張ですので、トートロジーなはずがないので除外されます。
http://blog.goo.ne.jp/lx2x5350/c/9a36178e64be7a6348b1eda82e5a9ce2
2015年(平成27年)国家公務員試験総合職二次試験 解答・解説 数理科学・物理・地球科学 専門(記述式) No1 Ⅱ (リーマンのゼータ関数・素数・自然数の逆数和)

解答
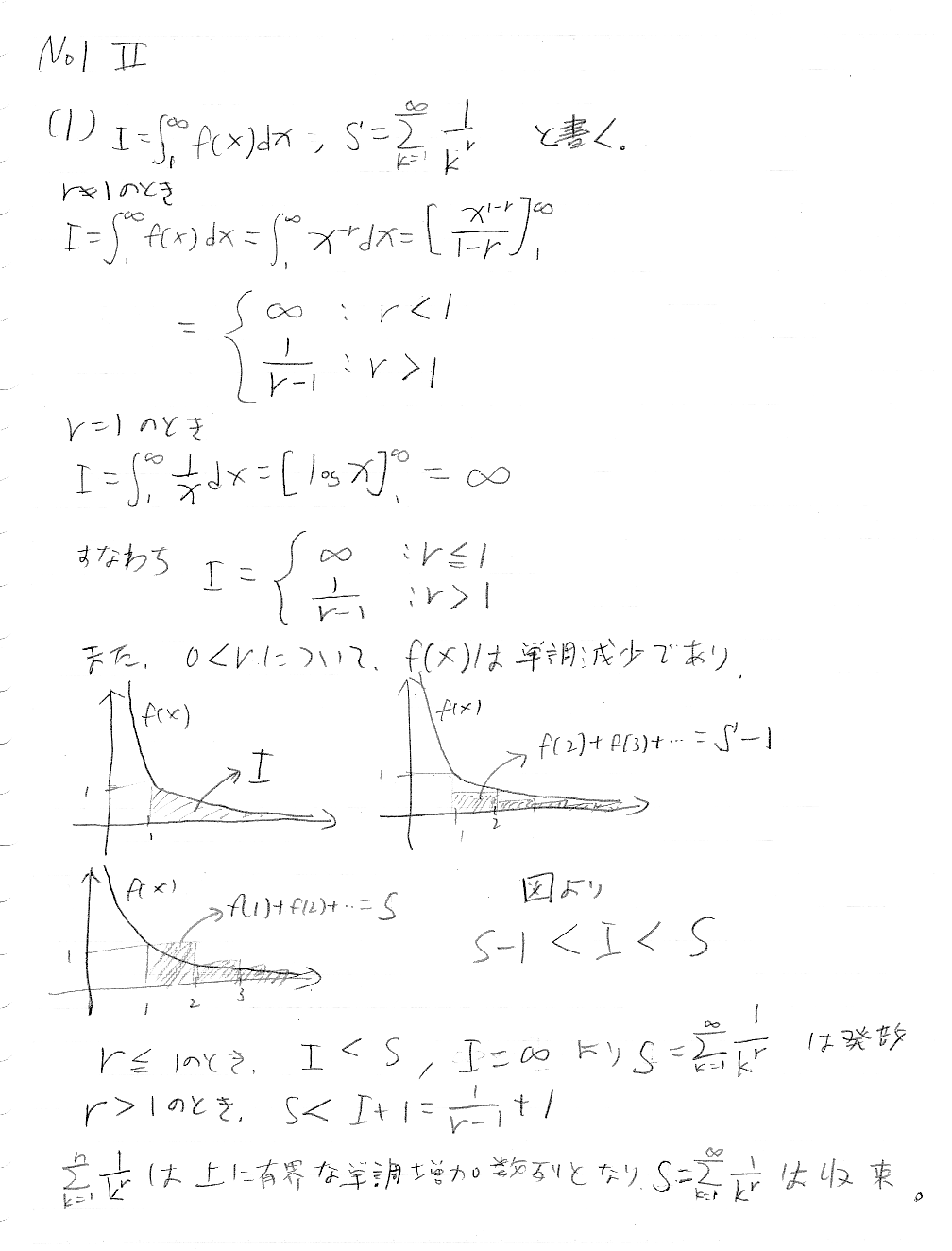

(1)の結果は、自然数の逆数の和(調和級数)が発散するという有名な命題を含んでいます。
また、
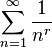 はr>1において収束しますが、
はr>1において収束しますが、
これはリーマンのゼータ関数の(1より大なる実数での)定義となっています。
リーマンのゼータ関数と素数の関係で、オイラー積
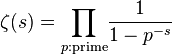 がありますが、これを示すのに(2)とほぼ同じ変形が現れます。
がありますが、これを示すのに(2)とほぼ同じ変形が現れます。
http://blog.goo.ne.jp/lx2x5350/c/9a36178e64be7a6348b1eda82e5a9ce2その他過去問一覧