ある方が、次の極限値(nC[n/2] / (2^n))を求めたいようでした。
以下のように証明をしてみました。
[n] : ガウス記号
n!! : 2重階乗
===== ここから =====
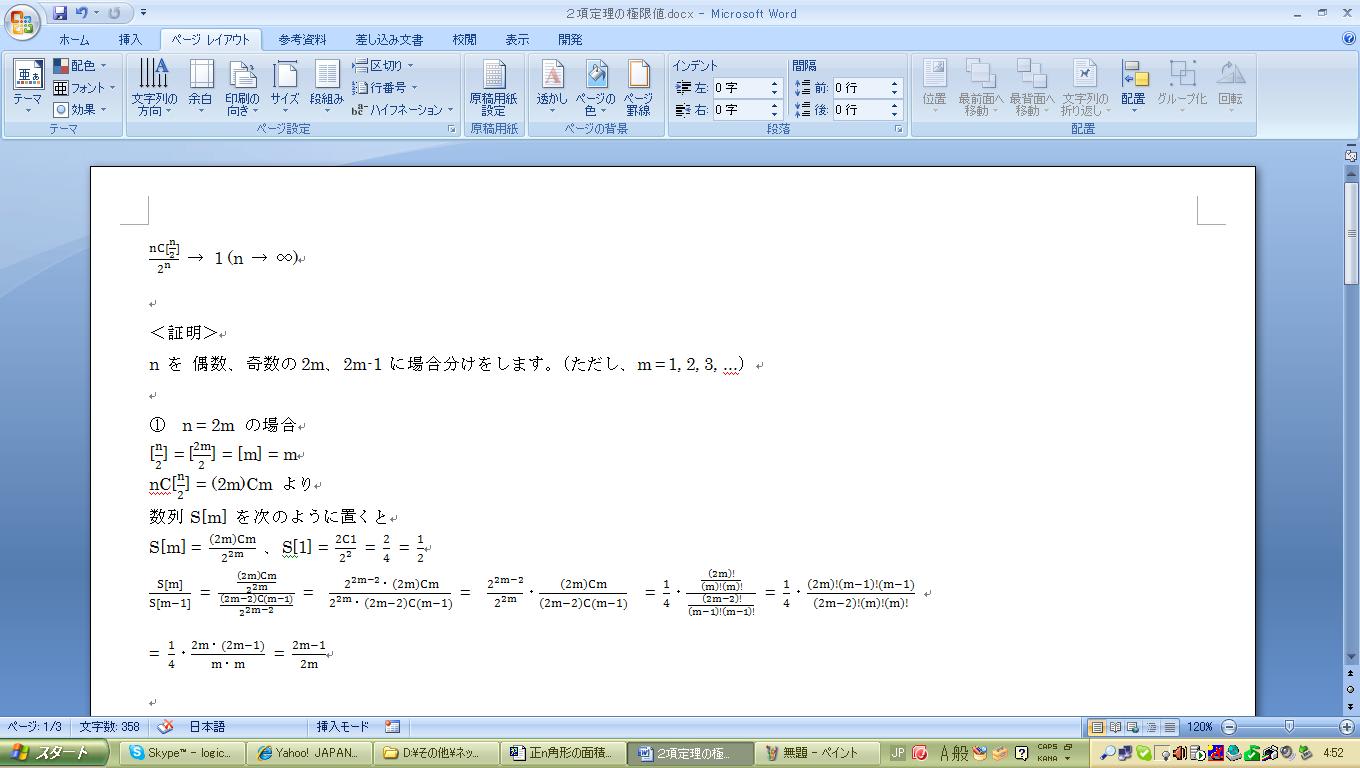
nC[n/2] / (2^n) → 1 (n → ∞)
極限値は「0」ではなく、「1」になります。
<証明>
n を 偶数、奇数の 2m、2m-1 に場合分けをします。(ただし、m = 1, 2, 3, ...)
① n = 2m の場合
[n/2] = [2m/2] = [m] = m
nC[n/2] = (2m)Cm より
数列 S[m] を次のように置くと
S[m] = (2m)Cm / {2^(2m)}
S[1] = 2C1 / (2^2) = 2 / 4 = 1 / 2
S[m] / S[m-1]
= [(2m)Cm / {2^(2m)}]/[(2m-2)C(m-1) / {2^(2m-2)}]
= {2^(2m-2)・(2m)Cm} / {2^(2m)・(2m-2)C(m-1)}
= {2^(2m-2)/2^(2m)}・{(2m)Cm / (2m-2)C/(m-1)}
= (1/4)・([(2m)!/{(m)!(m)!}] / [(2m-2)!/{(m-1)!(m-1)!}])
= (1/4)・([{(2m)!(m-1)!(m-1)!} / {(2m-2)!(m)!(m)!}])
= (1/4)・[{(2m)・(2m-1)} / {m・m}]
= (2m-1) / (2m)
②n = 2m-1 の場合
[n/2] = [(2m-1)/2] = [m - 1/2] = [(m-1) + 1/2] = m-1
nC[n/2] = (2m-1)C(m-1) より
数列 T[m] を次のように置くと
T[m] = (2m-1)C(m-1) / {2^(2m-1)}
T[1] = 1C1 / (2^1) = 1 / 2
T[m] / T[m-1]
= [(2m-1)C(m-1) / {2^(2m-1)}]/[(2m-3)C(m-2) / {2^(2m-3)}]
= {2^(2m-3)・(2m-1)C(m-1)} / {2^(2m-1)・(2m-3)C(m-2)}
= {2^(2m-3)/2^(2m-1)}・{(2m-1)C(m-1) / (2m-3)C/(m-2)}
= (1/4)・([(2m-1)!/{(m-1)!(m)!}] / [(2m-3)!/{(m-2)!(m-1)!}])
= (1/4)・([{(2m-1)!(m-2)!(m-1)!} / {(2m-3)!(m-1)!(m)!}])
= (1/4)・[{(2m-1)・(2m-2)} / {m・(m-1)}]
= (2m-1) / (2m)
①、②より
S[m] / S[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
S[1] = 1/2
T[m] / T[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
T[1] = 1/2
よって、偶数、奇数は
X[m] / X[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
X[1] = 1/2
より同じ数列になることが分かる。
X[m] = {(2m-1) / (2m)}・X[m-1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・X[m-2]
.....
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・X[2]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・X[1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・{1/2}
X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) ・・・(2)
nC[n/2] / (2^n) = X[m] より
nC[n/2] / (2^n) → 1 (n → ∞)
Q.E.D.
===== ここまで =====


(1) 証明の不備があれば、教えてください。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
どこからの本からの引用ではないので、極限値を確かめる方法がないため。
証明が合っているか、ないかを見て欲しいので、全内容を書きました。
※丸投げの意図ではなく、確認のためです。
※全内容は、自力で考えた内容です。
私の不安点は、(2)の部分です。
もし、この証明が合っていたならば、(1 + 1)^n = 2^n のとき、
(1 + 1)^n の最大値の nC[n/2] のとき、
nC[n/2] < (1 + 1)^n ⇔ nC[n/2] < 2^n なので、nC[n/2] / (2^n) < 1
でも、極限値は nC[n/2] / (2^n) → 1 (n → ∞) となる、不思議な結果になります。
===== 2012/01/11 AM9:25 追記 =====
数学のコミュに質問をしたら、丁寧に教えて頂きました。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
Wallis 積分から
(2m-1)!! / (2m)!! = (2/π) ∫_0^(π/2) (sin x)^(2m) dx → 0 (m → ∞)
X[m] → 0 (m → 0)より
nC[n/2] / (2^n) → 0 (n → ∞)
Wallis 積分は、とても勉強になりました。
以下のように証明をしてみました。
[n] : ガウス記号
n!! : 2重階乗
===== ここから =====
nC[n/2] / (2^n) → 1 (n → ∞)
極限値は「0」ではなく、「1」になります。
<証明>
n を 偶数、奇数の 2m、2m-1 に場合分けをします。(ただし、m = 1, 2, 3, ...)
① n = 2m の場合
[n/2] = [2m/2] = [m] = m
nC[n/2] = (2m)Cm より
数列 S[m] を次のように置くと
S[m] = (2m)Cm / {2^(2m)}
S[1] = 2C1 / (2^2) = 2 / 4 = 1 / 2
S[m] / S[m-1]
= [(2m)Cm / {2^(2m)}]/[(2m-2)C(m-1) / {2^(2m-2)}]
= {2^(2m-2)・(2m)Cm} / {2^(2m)・(2m-2)C(m-1)}
= {2^(2m-2)/2^(2m)}・{(2m)Cm / (2m-2)C/(m-1)}
= (1/4)・([(2m)!/{(m)!(m)!}] / [(2m-2)!/{(m-1)!(m-1)!}])
= (1/4)・([{(2m)!(m-1)!(m-1)!} / {(2m-2)!(m)!(m)!}])
= (1/4)・[{(2m)・(2m-1)} / {m・m}]
= (2m-1) / (2m)
②n = 2m-1 の場合
[n/2] = [(2m-1)/2] = [m - 1/2] = [(m-1) + 1/2] = m-1
nC[n/2] = (2m-1)C(m-1) より
数列 T[m] を次のように置くと
T[m] = (2m-1)C(m-1) / {2^(2m-1)}
T[1] = 1C1 / (2^1) = 1 / 2
T[m] / T[m-1]
= [(2m-1)C(m-1) / {2^(2m-1)}]/[(2m-3)C(m-2) / {2^(2m-3)}]
= {2^(2m-3)・(2m-1)C(m-1)} / {2^(2m-1)・(2m-3)C(m-2)}
= {2^(2m-3)/2^(2m-1)}・{(2m-1)C(m-1) / (2m-3)C/(m-2)}
= (1/4)・([(2m-1)!/{(m-1)!(m)!}] / [(2m-3)!/{(m-2)!(m-1)!}])
= (1/4)・([{(2m-1)!(m-2)!(m-1)!} / {(2m-3)!(m-1)!(m)!}])
= (1/4)・[{(2m-1)・(2m-2)} / {m・(m-1)}]
= (2m-1) / (2m)
①、②より
S[m] / S[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
S[1] = 1/2
T[m] / T[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
T[1] = 1/2
よって、偶数、奇数は
X[m] / X[m-1] = (2m-1) / (2m) (ただし、m = 1, 2, 3, ...)
X[1] = 1/2
より同じ数列になることが分かる。
X[m] = {(2m-1) / (2m)}・X[m-1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・X[m-2]
.....
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・X[2]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・X[1]
X[m] = {(2m-1) / (2m)}・{(2m-3) / (2m-2)}・.....・{5/6}・{3/4}・{1/2}
X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) ・・・(2)
nC[n/2] / (2^n) = X[m] より
nC[n/2] / (2^n) → 1 (n → ∞)
Q.E.D.
===== ここまで =====



(1) 証明の不備があれば、教えてください。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
どこからの本からの引用ではないので、極限値を確かめる方法がないため。
証明が合っているか、ないかを見て欲しいので、全内容を書きました。
※丸投げの意図ではなく、確認のためです。
※全内容は、自力で考えた内容です。
私の不安点は、(2)の部分です。
もし、この証明が合っていたならば、(1 + 1)^n = 2^n のとき、
(1 + 1)^n の最大値の nC[n/2] のとき、
nC[n/2] < (1 + 1)^n ⇔ nC[n/2] < 2^n なので、nC[n/2] / (2^n) < 1
でも、極限値は nC[n/2] / (2^n) → 1 (n → ∞) となる、不思議な結果になります。
===== 2012/01/11 AM9:25 追記 =====
数学のコミュに質問をしたら、丁寧に教えて頂きました。
(2) X[m] = {(2m-1)!! / (2m)!!} → 1 (m → ∞) は、言いきっても良いでしょうか?
Wallis 積分から
(2m-1)!! / (2m)!! = (2/π) ∫_0^(π/2) (sin x)^(2m) dx → 0 (m → ∞)
X[m] → 0 (m → 0)より
nC[n/2] / (2^n) → 0 (n → ∞)
Wallis 積分は、とても勉強になりました。









