どんな分割が純正律の良い近似なのか?
(1)近似の対象
色々な考え方があると思いますが、私は大全音・小全音・ディアトニック半音の大きさの近似が良いものと言う基準で探しました。
(↑他にたとえば純正完全五度・純正長三度の大きさや6つの幹音のCからの距離など。)
(2)近似の評価その1
(1)の方法で言えば
オクターブ = 大全音*3 + 小全音*2 + ディアトニック半音*2
とならない分割は論外です。
悪い例として500分割で近似してみます。
大全音 = 203.910セント = 84.963/500オクターブ ≒ 85/500オクターブ
小全音 = 182.404セント = 76.002/500オクターブ ≒ 76/500オクターブ
ディアトニック半音 = 111.731セント = 46.555/500オクターブ ≒ 47/500オクターブ
500 ≠ 85*3 + 76*2 + 47*2 = 255+152+94 = 501
(3)近似の評価その2
正確な値の小数部が0.5に近ければ近いほど悪いのはすぐ予想がつくと思います。以下1200分割の例を挙げていきます。
203.910 - int(203.910) = 0.910
182.404 - int(182.404) = 0.404
111.731 - int(111.731) = 0.731
「(正確な値-近似値)の絶対値が小さいほど良い」と言いかえます。後の計算のため。
abs(203.910 - round(203.910, 0)) = abs(203.910 - 204) = 0.090
abs(182.404 - round(182.404, 0)) = abs(182.404 - 182) = 0.404
abs(111.731 - round(111.731, 0)) = abs(111.731 - 112) = 0.269
この三つの中で最も近似の良くない(大きい)値を選びます。
max(0.090, 0.404, 0.269) = 0.404
ここで加算耐性(仮)なるローカル用語を使います。
加算耐性(仮) = 1/((正確な値-近似値)の絶対値)/2
1/0.404/2 = 1.239 (1.239は1より大きく2より小さい)
↑の()内の意味は
(正確な値*1)の近似値 = 近似値*1
(正確な値*2)の近似値 ≠ 近似値*2
です。
round(182.404*1, 0) = 182 = round(182.404, 0)*1 = 182
round(182.404*2, 0) = 365 ≠ round(182.404, 0)*2 = 364
((↑ミスを訂正しました。ディアトニック半音の例 -> 小全音の例 h260322)
(4)近似の評価その3
「(正確な値-近似値)の絶対値」が同じなら分割数が大きい方が無駄、という考え方を採用します。
(大きい方が正確な値に近いはずですが、扱う桁数を減らすのが近似の目的ならば本末転倒ということで。)
その考え方を表現する一つの例が次の式です。
効率(仮) = 加算耐性(仮)^2/分割数
とても恣意的な式です。いろいろと試してみて上位に来て欲しい分割数が上位に来るように選んだ後付けの式です。
(5)近似の評価その4
以上の計算を表にしました。分割数は12から1224まで。借り物の空間なので少し遠慮しました ^^
(表7) 並べ替え前
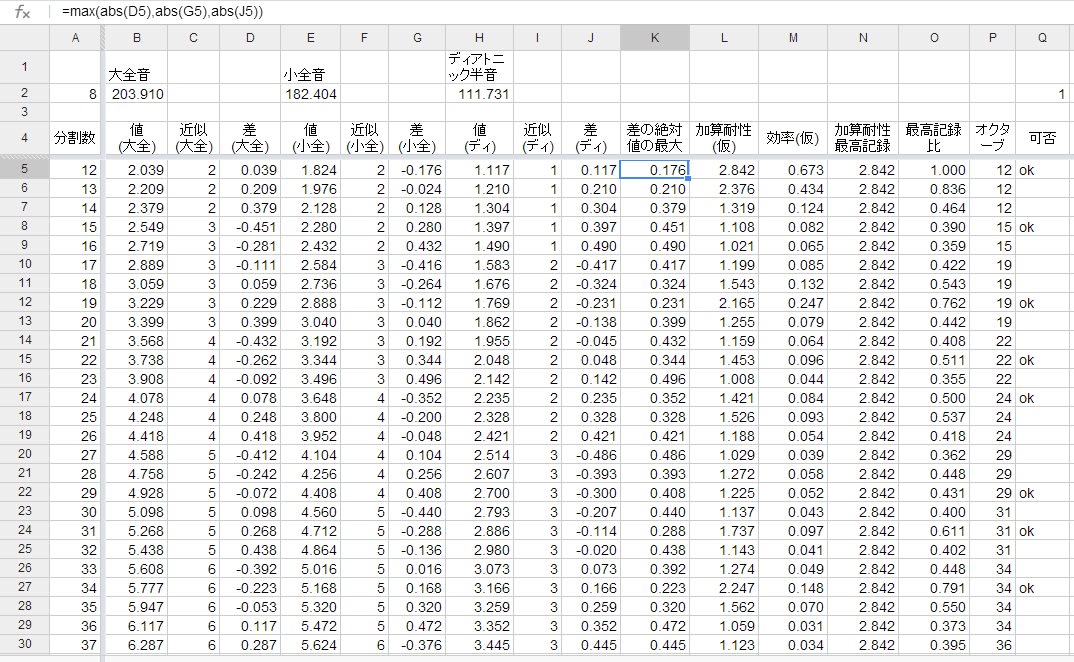
(表8) 並べ替え後
効率(仮)が大きい順に並べ替えました。論外の13分割が5位に来ました。効率(仮)が0.5未満は無視しても良いような気がします。

↓は総当たり戦で約200万分割まで計算して効率(仮)が0.5以上のものを集めたものです。(↓ h260605修正 htmlのtableを使って揃えてみました)
| 効率(仮) | 加算耐性(仮) | 分割数 | 備考 |
| 2.080 | 94.527 | 4296 | 12の倍数で桁数もほどほどなので近似に便利かも |
| 2.053 | 3735.134 | 6796263 | これだけは検索で他サイトから借りてきました ^^; |
| 1.884 | 383.382 | 78005 | |
| 1.110 | 7.668 | 53 | 一部の人々に流行っている分割? |
| 0.817 | 1010.989 | 1251764 | セント値を小数点以下3桁覚えると思えば頑張れるかも(笑) |
| 0.673 | 2.841 | 12 | 最も基本的な分割 |
| 0.609 | 19.310 | 612 | 12の倍数で桁数もほどほどなので近似に便利かも |
| 0.550 | 355.536 | 229719 | |
| 0.523 | 7.857 | 118 |
「6796263」の参照元サイト:「12 53 612 4296 1251764」で検索、7番目に表示されました。Kees tuning pages 総当たりではなく適格な理論的アプローチのようです。(追記r060324)























