3の33乗はどうやって計算すべきか? - ザリガニが見ていた...。 に触発されて、また大きなケタの除算を、電卓を使って計算してみる - GameSprit の無駄な快感を忘れられずに、3の33乗を計算してみた。
道具は、電卓と紙と鉛筆。「3の33乗はどうやって計算すべきか? - ザリガニが見ていた…。」 のリンク先(数学教師「バカ正直に計算して合ってたのはお前だけだ」... on Twitpic)にあるように、1つずつ手計算するのも1つの方法だとは思うが、計算回数が増えると間違いも増える。
まず、手元の8ケタ電卓でどこまで計算できるかを敢えて確認してみる。
3^1 = 3
3^2 = 9
3^3 = 27
3^4 = 81
3^5 = 243
3^6 = 729
3^7 = 2,187
3^8 = 6,561
3^9 = 19,683
3^10 = 59,049
3^11 = 177,147
3^12 = 531,441
3^13 = 1,594,323
3^14 = 4,782,969
3^15 = 14,348,907
3^16 = 43,046,721
3^17 = 1.2914016e …
ちなみに、電卓では「3 × × =」で「9」が表示され、以降は「=」を押すたびに「27」「81」「243」「729」「2,187」「6,561」「19,683」「59,049」「177,147」「531,441」「1,594,323」「4,782,969」「14,348,907」「43,046,721」「1.2914016e」が表示される。
そして、答えの桁数がどれくらいかを確認してみよう。
これはリンク先「3の33乗はどうやって計算すべきか? - ザリガニが見ていた…。」が結論を出してくれている。
結論として、3の33乗の答えは16ケタとなる。
ここで、3^33を分解し計算回数を少なくしてみよう。
いくつかのパターンを考えてみる。
(1) 3^33 = 3^30 * 3^3 = 3^15 * 3^15 * 3^3
(2) 3^33 = 3^25 * 3^8 = 3^10 * 3^15 * 3^8
計算してゆく桁に注目する。
(1) 8ケタ * 8ケタ * 2ケタ 14,348,907 * 14,348,907 * 27
(2) 5ケタ * 8ケタ * 4ケタ 59,049 * 14,348,907 * 6,561
どちらもできないことはないが、各桁の数字に繰返しが少ないので、計算量が多くなりそう。
そこで、3^16までの結果を振り返って、なるべく同じ数字で構成されたものに注目してみる。
おっ! 3^11がいいんじゃないか! 「177,147」これなら1,4,7の3つの数字で構成されているので、
計算結果を使い回しすることで計算量を減らすことができる。
(3) 3^33 = 3^11 * 3^11 * 3^11 = 177,147 * 177,147 * 177,147
で、(3)に決めて、177,147 に 1,4,7を掛けた結果を見てみる。
177,147 * 1 = 177,147
177,147 * 4 = 708,588
177,147 * 7 = 1,240,029
これを使って、177,147 * 177,147を計算する。
上の計算の結果を書き込み、タテの足し算は6ケタ毎に電卓を叩く。
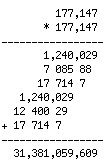
240,029 + 85,880 + 714,700 + 29,000 + 290,000 + 700,000 = 2,059,609
1 + 7 + 17 + 1,240 + 12,400 + 17,714 = 31,379
31,379 * 1,000,000 + 2,059,609
= 31,381 * 1,000,000 + 59,609
= 31,381,059,609
結果を、(3)の式に当てはめてみる。
(3 -a) 3^33 = 3^11 * 3^11 * 3^11 = 31,381,059,609 * 177,147
ふたたび、31,381,059,609に1,4,7を掛ける。
31,381,059,609 * 1 = 31,381,059,609
31,381,059,609 * 4 = (31,381 * 1,000,000) * 4 + 59,609 * 4 = 125,524 * 1,000,000 + 238,436 = 125,524,238,436
31,381,059,609 * 7 = (31,381 * 1,000,000) * 7 + 59,609 * 7 = 219,667,000,000 + 417,263 = 219,667,417,263
これを使って、31,381,059,609 * 177,147を計算する。
同様に書き込み、タテの加算は6ケタ毎に電卓を叩く。

結論です。
3^33
= 3^11 * 3^11 * 3^11
= 177,147 * 177,147 * 177,147
= 31,381,059,609 * 177,147
= 5,559,060,566,555,523
キーワード:巨大数、大きなケタ、掛け算、乗算、3の33乗
道具は、電卓と紙と鉛筆。「3の33乗はどうやって計算すべきか? - ザリガニが見ていた…。」 のリンク先(数学教師「バカ正直に計算して合ってたのはお前だけだ」... on Twitpic)にあるように、1つずつ手計算するのも1つの方法だとは思うが、計算回数が増えると間違いも増える。
まず、手元の8ケタ電卓でどこまで計算できるかを敢えて確認してみる。
3^1 = 3
3^2 = 9
3^3 = 27
3^4 = 81
3^5 = 243
3^6 = 729
3^7 = 2,187
3^8 = 6,561
3^9 = 19,683
3^10 = 59,049
3^11 = 177,147
3^12 = 531,441
3^13 = 1,594,323
3^14 = 4,782,969
3^15 = 14,348,907
3^16 = 43,046,721
3^17 = 1.2914016e …
ちなみに、電卓では「3 × × =」で「9」が表示され、以降は「=」を押すたびに「27」「81」「243」「729」「2,187」「6,561」「19,683」「59,049」「177,147」「531,441」「1,594,323」「4,782,969」「14,348,907」「43,046,721」「1.2914016e」が表示される。
そして、答えの桁数がどれくらいかを確認してみよう。
これはリンク先「3の33乗はどうやって計算すべきか? - ザリガニが見ていた…。」が結論を出してくれている。
3^33 = (10^0.4771)^ 33 = 10^(0.4771×33) = 10^15.7443
=10^0.7443 × 10^15
10^1未満は必ず10未満の数になるので、1桁。
上記に10^15を掛算すると0が15個追加され16桁になる。
ゆえに...
3の33乗は何桁の整数か?
16桁の整数。
結論として、3の33乗の答えは16ケタとなる。
ここで、3^33を分解し計算回数を少なくしてみよう。
いくつかのパターンを考えてみる。
(1) 3^33 = 3^30 * 3^3 = 3^15 * 3^15 * 3^3
(2) 3^33 = 3^25 * 3^8 = 3^10 * 3^15 * 3^8
計算してゆく桁に注目する。
(1) 8ケタ * 8ケタ * 2ケタ 14,348,907 * 14,348,907 * 27
(2) 5ケタ * 8ケタ * 4ケタ 59,049 * 14,348,907 * 6,561
どちらもできないことはないが、各桁の数字に繰返しが少ないので、計算量が多くなりそう。
そこで、3^16までの結果を振り返って、なるべく同じ数字で構成されたものに注目してみる。
おっ! 3^11がいいんじゃないか! 「177,147」これなら1,4,7の3つの数字で構成されているので、
計算結果を使い回しすることで計算量を減らすことができる。
(3) 3^33 = 3^11 * 3^11 * 3^11 = 177,147 * 177,147 * 177,147
で、(3)に決めて、177,147 に 1,4,7を掛けた結果を見てみる。
177,147 * 1 = 177,147
177,147 * 4 = 708,588
177,147 * 7 = 1,240,029
これを使って、177,147 * 177,147を計算する。
上の計算の結果を書き込み、タテの足し算は6ケタ毎に電卓を叩く。
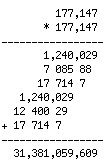
240,029 + 85,880 + 714,700 + 29,000 + 290,000 + 700,000 = 2,059,609
1 + 7 + 17 + 1,240 + 12,400 + 17,714 = 31,379
31,379 * 1,000,000 + 2,059,609
= 31,381 * 1,000,000 + 59,609
= 31,381,059,609
結果を、(3)の式に当てはめてみる。
(3 -a) 3^33 = 3^11 * 3^11 * 3^11 = 31,381,059,609 * 177,147
ふたたび、31,381,059,609に1,4,7を掛ける。
31,381,059,609 * 1 = 31,381,059,609
31,381,059,609 * 4 = (31,381 * 1,000,000) * 4 + 59,609 * 4 = 125,524 * 1,000,000 + 238,436 = 125,524,238,436
31,381,059,609 * 7 = (31,381 * 1,000,000) * 7 + 59,609 * 7 = 219,667,000,000 + 417,263 = 219,667,417,263
これを使って、31,381,059,609 * 177,147を計算する。
同様に書き込み、タテの加算は6ケタ毎に電卓を叩く。

結論です。
3^33
= 3^11 * 3^11 * 3^11
= 177,147 * 177,147 * 177,147
= 31,381,059,609 * 177,147
= 5,559,060,566,555,523
キーワード:巨大数、大きなケタ、掛け算、乗算、3の33乗