IDLでGauss fitting(ガウスフィッティング)を行う

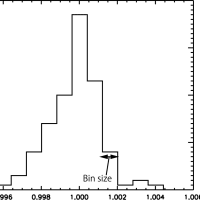
ガウス分布（正規分布）にIDLの組み込み関数を用い、フィッティングを行う。

result=gaussfit(x, y, a, nterms=3)

x : x軸の配列
y : y軸の配列
a : フィッティングした関数の定数が格納される
nterms : フィッティングを行う関数の種類。代入できる値は3,4,5,6のみ。
その他にもオプション有り。。。


因に、現在のフィッティング関数は以下の形式である。
f(x)=A*exp(-(z^2/2))
A : ガウス分布の高さ
z : (x-A1)/A2
A1 : ガウス分布の中心
A2 : ガウス分布の幅(標準偏差 σ)

ここから半値幅(半値全幅：FWHM)を導出するには次の式を用いる。
FWHM = s * sqrt( 2 * ln( 2 ) ) * A2　≒　2.35482*A2