コンデンサ、つなぎ替え

知恵袋 https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12295162197

初期条件：下図1

（C1=2μF:電圧20V、C2=1μF:電圧20V、C3=6μF:電圧0V）

 

▶【問い】スイッチをaにし、次にbにした時、C1の極板A側の電荷を求めよ。

またC3左極板の電荷の符号は➕か➖か？

 

▶解説

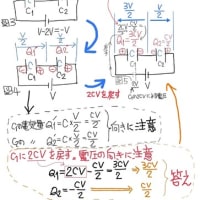
スイッチaにするとC1の電荷C1×20V=2×20=40μCはC3側へ分散するので、その結果

C1の電圧V1は下がり

C3の電圧V3は上がる

そして充分時間経過すると、ついにはV1=V3になる。つまり電位差=0になるので電荷の分散は止まり定常状態になる。この状態を電荷量の保存則を用いいて式にすると

40μC=C1V1+CV3=2×C1+1×V3

V1=V3なので、V1=3V3=V’とすると

40=2V’+6V’=8V’

V’を求めると

V’=40/8=5[V]

つまり

C1の電荷Q1=2×2=10μC、左極板が➕、電圧5V

C3の電荷Q3=6×5=30μC、左極板が➕、電圧5V

この時、 C2の電荷Q2=1×20×20μC、左極板が➕、電圧20V です。

 

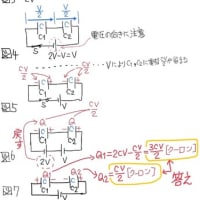
次にスイッチをbに切り替えると

C1,C2,C3は閉回路になり、C1の5VとC3の5Vは打ち消し合うので合成電圧は0V、だから閉回路の電圧は、等価的にC2の20V

この20VによりC1,C2,C3に溜まる電荷量Qは

Q={1/(C1+1/C2+1/C3)}×20

={1/(1/2+1/2+1/6)}×20

={1/(3/6+6/6+1/6)}×20

={1/(10/6)}×20

=(6/10)×20

=6×2

=12μC

この12μCの電荷が、C1,C2,C3から成る閉回路に、反時計回り方向へ流れるので（C1,C1,C3の各電荷の➕/➖と12μCが流れる方向を考慮して計算すると）

C1の電荷量Q1=10−12=−2μC、右極板が➕、電圧=2/2=1V

C2の電荷量Q2=20−12=8μC、左極板が➕、電圧=8/1=8V

C3の電荷量Q3=30+12=42μC、左極板が➕、電圧=42/6=7V

 

なので

C1の左極板Aの電荷量=−2 [μC]　…(答え)

C3の右極板の電荷の符号は➕　…(答え)