▶第3の解き方
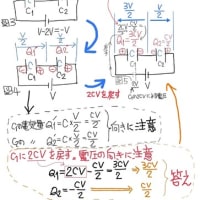
S1閉じ定常状態後のQ1,Q2は
(同じ電荷量Qなので、キルヒホッフの第2法則、電荷の公式V=Q/Cより)
30=V1+V2=Q/C1+Q/C2=Q×(1/1+1/2)=2Q/3より
Qを求めるとQ=Q1=Q2=30/(3/2)=20[μC]
S1開き、S2閉じ定常状態後のQ2,Q3は
(C2,C3は同じ電圧V[V]で定常状態になるので、孤立部分における電荷の保存則、電荷の公式Q=CVより)
Q=20=Q2+Q3=C2V+C3V=(2×V)+(3×V)=5×V [μC]より
(公式V=Q/Cを使ってVを求めると)V=20/5=4[V]
∴Q2=2×4⁼8μC、∴Q3=3×4=12μC
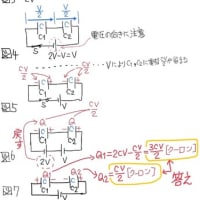
S2開き、S1閉じ定常状態後のQ1,Q2を求めると
(S1閉じる直前のC1,C2の電圧20V,4V
なので30Vとの電位差は) 30-20-4=6V
この6VによりC1,C2に新たに充電される電荷をQ’とすると
Q’=1×6×2/(1+2)=4[μC] (又は Q’=2×6×1/(1+2)=4[μC])
(この時、C1,C2は直列だから、この電荷量Q’=4μCが新たに追加されるので)
∴Q1=20+4=24[μC]
∴Q2=8+4=12[μC]
↑
こんな解法もありますよ、(^o^)ノ
▼つなぎ替え2

(1)、























※コメント投稿者のブログIDはブログ作成者のみに通知されます