
知恵袋: https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14297588484

▶答え
(1):(2/3)CV
(2):(4/15)CV
(3):(2/5)CV
▶別解
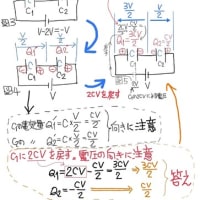
(1)、スイッチがaの時、
C, 2Cは直列で印加電圧=Vとして
(電荷の公式Q=CVよりV=Q/Cなので)
キルヒホッフの第2法則より
V=Q/C+Q/2C
=Q×(1/C+1/2C)
=Q×(3/2C)
=Q/(2C/3)
∴2Cの上極板の電気量Q=2CV/3=(2/3)CV …(答え)
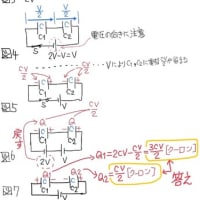
(2)、その後スイッチをbにすると
2Cの電圧=V/3なので、このV/3により直列の2C, 3Cに時計回り方向へ流れる電気量Q3とすると
(キルヒホッフの第2法則より)
V/3=Q3/2C+Q3/3C
=Q3×(1/2C+1/3C)
=Q3/(6C/5)
Q3を求めると
Q3=(V/3)×(6C/5)
=6CV/15
=2CV/5
∴2Cの上極板の電気量=2CV/3−2CV/5
=4CV/15
=(4/15)CV …(答え)
(3)、その後スイッチをaにすると
電源電圧V
Cの電圧=−2V/3
2Cの電圧=−2V/15
なので
電圧計=V−2V/3−2V/15
=3V/15
=V/5
なので、このV/5により直列のC, 2Cに時計回り方向へ流れる電気量Q2とするとキルヒホッフの第2法則より
V/5=Q/C+Q/2C
=Q×(1/C+1/2C)
=Q2/(2C/3)
Q2を求めると、Q2=(V/5)×(2C/3)
=2CV/15
∴2Cの上極板の電気量=4CV/15+2CV/15
=6CV/15
=2CV/5
=(2/5)CV …(答え)


















※コメント投稿者のブログIDはブログ作成者のみに通知されます