図１ 光電効果
金属に光を照射すると、電子が金属から叩き出される。この現象は、光が振動数に比例するエネルギーを持つ粒子であることを示す。ある振動数以上の光を当てると電子が飛び出し、同じ振動数の光を強く当てると飛び出す電子の数も増える。振動数の小さい光をどんなに強くしても、電子は飛び出さない。
このメモは、自然界にある４つの力を記述するのが第１目標。その結果、素粒子についても書いている。だが、これまで吹っ飛ばしてしまったことも多い。反粒子、スピン、量子数、保存量、できればアイソスピンなどをメモっておかないと、これからの話はわけが分からなくなりそうだ。そこで、反粒子とスピンの話に入りたいのだが、それには相対論的量子力学という難問が立ちはだかる。
(1) 量子力学
アインシュタインによる光電効果の発見（1905年、図１）によって、光がhν (h はプランク定数、ギリシャ文字の ν [ニュー]、以下ギリシャ文字は赤で表す。) を１単位とするエネルギーの粒（つまり量子）の集まりであるということが分かった。その後、ド・ブロイの物質波の提案や電子の波動性の発見によって、量子の概念が光だけでなく他の物質にも広く成り立つことが分かった。
量子力学の目的は、量子の波動関数（波の形状）を決定することである。例えば１次元だけで考えると、量子はまず粒子性があるはずなので、その運動エネルギーは p を粒子の運動量、m を質量として、
E = (1/2) p2/m + V(x) ①
と表せる。V(x) は位置エネルギーや電場のエネルギーであり、総称してポテンシャルエネルギーという。
振動数 ν と波長 λ ［ラムダ]の波動関数 Ψ[プサイ]は、
ψ(x, t) = A cos [ 2π (x/λ - νt) ] ②
と表せる。π[パイ]は円周率。
.jpg)
量子１つのエネルギーは E = hν であり ド・ブロイの関係式 p = h/λ で、①と②が関連づけられる。①を満たす②を求めることが量子力学のほぼすべてであると言って構わない。結局それは、ある偏微分方程式をとくということに帰着した。シュレーディンガーが、この方程式を編み出したのは、1926年とされる。ポテンシャルエネルギーの項を無視すると、１次元のシュレーディンガー方程式は、図２のようになる。
この図にある h に横線を重ねた記号はエイチ・バー ħ （又はディラック定数）と呼ばれるが、プランク定数 h を 2π で割った値。この解である波動関数 Ψ の絶対値の２乗が、x 地点での粒子の存在確率である。１次元を３次元に拡張するとか、ポテンシャルエネルギーの形をいろいろ変えたりた境界条件に対して、いろいろなシュレーディンガー偏微分方程式ができ、それぞれ違った解（波動関数 Ψ ）が求まる。やってみると式が複雑な上に、記号や添字も多くて間違いやすく、最後までたどり着くのは至難のワザである。
しかし、光速近くで飛び回る粒子のことなどは、この方程式では考慮されていない。加速器実験などに量子力学を当てはめることは無理であった。光速近い粒子では、特殊相対論を考慮した方程式が必要なのである。「波動関数はシュレーディンガーの方程式に従うが、これはニュートンの古典力学を量子力学的に翻訳したものだから、特殊相対論の枠の中には入っていない。すなわちシュレーディンガーの方程式は非相対論的な量子力学にとどまっているものである。[1]」 ここでいう相対論とは、アインシュタインの特殊相対性理論である。
(2) 特殊相対性理論
この理論の最初の柱は、「光速度不変の原理」である。光速は c = 3.00 x 108 m/s である。（実際には端数があり、真空中か空気中かでも値は異なるが、とりあえずその点は無視する。） 時速1000km/s (106 m/s)で走行できる車があったとして、ヘッドライトを点灯するとその光の速度は、道端に止まっている人から見ると3.01 x 108m/s （光の速度＋ヘッドライト自体の移動速度）となる。 仮に車が光速で走れば、 道端に止まっている人から見ると 6.00 x 108ms というのがニュートン力学の常識であった。
しかし、どちらの場合も、光の速度は3.00 x 108ms ポッキリなのである。 つまり光速度は不変である。有名なマイケルソン・モーリーの実験は、（実験者の当初の意図を裏切って）このことを確かめる結果となったのであった。
このことはあまりに常識ハズレなので、簡単には納得できない。納得できずに「アインシュタインは大嘘つき」と結論づける人もいる（最近はすくないか？）。特殊相対性理論の解説本などには、分かりやすいはずの『思考実験』[2]などが載っているが、かなり注意深く読まないと誤解してしまう（書き手の先生もずいぶん気を使うだろうなー）。
特殊相対性理論にもとづき、慣性系が違っても（つまり車や新幹線どころか、亜光速ロケットに乗っていても道端に止まっていても）、光速度が不変なことを以下に説明してみよう。
特殊相対性理論によると、ある一定の相対速度で運動している２つの慣性系AとBがあるとする。A系からB系を見た場合でも、B系からA系を見た場合でも、相手の慣性系の時間の進みは遅く、距離は縮んで見える。A系から見るとB系の距離は極端に縮んでおり、時間の進みも極端に遅れている。B系での距離⊿x は A系から見ると ⊿x/γ に縮む。B系での時間間隔 ⊿t は A系から見ると ⊿ｔ・γ に伸びる。このγ[ガンマ]はA系とB系との間の相対速度 v と光速 c によって、次のように表される【注１】。
γ = 1/(1 - v2/c2)1/2 (γ>1) ③
仮に A系からみてB系が v= 2.99 x 108m/s で遠ざかりながら、さらにB系の前方に光を発したとする。それぞれの系での光の速度はどうなるであろうか？A系、B系それぞれの内部ではもちろん3.00 x 108m/s だが、A系から見たB系の光速度はそうではない。単位速度は(⊿x・γ)/(⊿ｔ/γ) = (⊿ｘ/⊿t)・γ2 だから γ の２乗倍になる。つまり単位速度（例えば 1 km/s）が大きくなるので、速度の値自体は小さくなるのだ。このために、光の速度もノロノロなのだ。A系からB系がある方向に移動し、B系では同じ方向に光を発したとする。このときA系から見たB系の光の速度は、[A系とB系の相対速度 2.99 x 108m/s] + [B系の光速度]となるが、この和がどうやっても 3.00 x 108m/s なのである。つまりA系から見たB系の光速度は 0.01 x 108m/s というノロノロなのである。A系とB系を取り替えても話は同じ。（この部分の説明に関しては必ず【注２】を参照のこと。）
光速度不変の原理とはこのことである。 ついでに言うと、いろいろな本に時間の進みが遅れることを「時計が遅れる」と表現しているが、これは単なる比喩ではない。B系を含めあらゆる慣性系内部では、物理法則は正常に働く（「特殊相対性原理」といい、特殊相対性理論の第２の柱）から時計も正しい。ところがA 系から見たらその時計は遅れているのである。
(3) 相対論的量子力学
シュレーディンガー方程式では、特殊相対性理論を考慮していない。「シュレーディンガー方程式では、時間については１階微分、空間座標については２階微分という形になっていて、これでは時間と空間がばらばらなのは最初から明らかだ。すぐにわかることだが、そもそもの原因は、出発点として使った関係式 E=(1/2)p2/m が相対論を考慮していないことにある。[3]」
相対論を考慮するとエネルギーと運動量の関係は E=(1/2)p2m でなく、
E2=(pc)2 + (mc2)2 ④
となる。この式の説明は①の代わりに④を使って、波動関数を求める偏微分方程式をつくると、図３（クライン・ゴルドン方程式）になり、ここでは 時間も空間も２階微分になる。しかし、時間が２階微分になると、波動関数 Ψ の絶対値の２乗が粒子の存在確率であるということが成り立たないらしく、存在確率がマイナスになる。「ここに粒子が現れる確率がマイナス20パーセント、などというバカな話はありえない[3]」
そこで、「天才ポール・ディラックのアクロバット[3]」が行われた。彼はE2=(pc)2 + (mc2)2 を無理やり、
E=(α1p1+α2p2+α3p3)c + βmc2 ⑤
と書き直してしまい、そして⑤を２乗すれば④になるように3つのアルファ α1、α2、α3、とベータβ を決めた。①の代わりに④を使って、波動関数を求める偏微分方程式をつくると、図４（ディラック方程式）になり、ここでは時間も空間も１階微分になる。絶対値の２乗で、粒子の存在確率を表すこもできた。ディラックがこの方程式を考案したのは、1928年のことである。シュレディンガー方程式から、たった２年あとである。
南部陽一郎は、このディラックの業績を次のように評価している。
「ディラックの方程式はシュレーディンガーの方程式にはなかった新しい性質をいろいろ含んでいる。・・・電子のスピンはディラックが初めて導き出したのではなく、それ以前に原子のスペクトルを説明するために仮定されていたものであるが、ディラック方程式から自動的に出てきたことは、相対論的量子力学の輝かしい勝利であった[1]」
「スピン以外にもう１つディラック方程式のもたらした新しい結果は「反電子」または普通「陽電子」と呼ばれている粒子の存在である。[1]」陽電子は最初に見つかった反粒子であるが、この段階では理論の上での発見であった。
[1] 南部陽一郎 「クォーク 第２版」 1998年 講談社ブルーバックス p. 63-64
[2] 大栗博司 「重力とは何か」 幻冬舎新書 2012年 p.64-73
[3] 橋本省二 「質量はどのようにして生まれるのか」 2010年 講談社ブルーバックス p. 98-100
［下］慣性系 F は速度 −v でF′ の x′軸方向に動く（逆変換）
【注１】この γ[ガンマ] を「ローレンツ因子」という。β[ベータ] = v/c と書いて、γ = (1 - β)1/2 という表記もよく見かける。
ヘンドリック・ローレンツはマイケルソン・モーリーの実験結果（つまり光速度不変）に対応して、電磁気学のマックスウェル方程式がどの慣性系でも成り立つようにするために、それまでの「ガリレイ変換」に代わる「ローレンツ変換」という慣性系の座標変換規則を導出した。
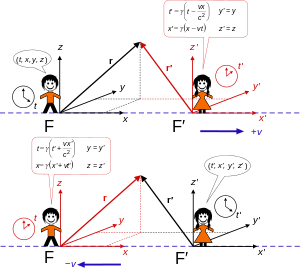
この変換は４次元の静止系 F ( x, y, z, t ) とそれに対して x 軸方向へ速度 v で運動している系 F' ( x', y', z', t' ) の間の関係式を求める。t = 0 の瞬間、両者の原点は一致していたとする。 この同じ t = 0 の瞬間、F 系の原点から光が放たれたとするとこの光は全方向に飛び去って、t 秒後には原点から半径 ct だけ離れた球面上の点に分布するはずである。これを式で表せば、
x2 + y2 + z2 = (ct)2 (1)
となる（球面の方程式）。
一方、 F' 系の原点にいる観測者にも光が光速c で同心円状に広がる。
x'2 + y'2 + z'2 = (ct')2 (2)
F 系から F' 系への変換を求めるというのは、(1) と (2) の条件のもとで、{x' , y', z', t'} = [A]{x, y, z, t} となるような行列[A]を求めることであり、ローレンツ変換はその答である。実際には A の要素はほとんど０なので、行列表現よりも数式で表現されることが多い。彼はこの過程で「ローレンツ収縮 ⊿x/γ」や「時間の遅れ」も発見していた。「収縮」はフィッツジェラルドも独自に仮説化していたので、「フィッツジェラルド・ローレンス収縮」ともいう。これらは1985年～1905 年のことであり、アインシュタインが1905 年に発表した特殊相対性理論は彼１人の功績ではない。（ローレンツは電磁気学の「ローレンツ力（電磁場中で運動する荷電粒子が 受ける力）」にも、その名前を残している。）
【注２】速度の合成に関するこの説明は、私のオリジナルであるが、実は間違っている。この論理では、A系から見たB系の速度は (dｌγ)/(dt/γ) = (dl/dt)γ2である。dl/dt = c とすると 見かけ速度は cγ2、 合成速度 V = v + cγ2 = v + c - v2/c である。これは近いけれども c ではない。正しくない答である。特殊相対性理論にもとづく速度の合成側はとっくの昔に定式化されており、 V = (vA + vB)/(1 + vAvB/c2)。それを当てはめると、vA = v、vB= c として、V = (v + c)/(1 + vc/c2) = (v + c) /(1 + v/c) = (v + c) / ((c + v) /c) = c (v + c)/(v + c) = c となり何の問題もない。もちろん、これが正しいのだ。しかし、私の解釈はどこが間違っているのか分からないので、現時点はこのまま載せておく。間違いの究明は後日の楽しみにする。
【注３】E2=(pc)2 + (mc2)2 という式の意味はなにか？
相対性理論では３次元の空間では、４次元の時空間で考える。いま w = ct として、各慣性系においては w2 - x2 - y2 - z2 は不変量（ローレンツ変換によって値の変わらない量）である。この値の微小変化を、τ[タウ] という文字を導入して、
(dτ)2 = (dw)2 -(dx)2 - (dy)2 - (dz)2 [A]
と書けば、dτ は微小時間 dt の間に微小距離 dx, dy, dz だけ移動した場合の、４次元空間内での移動距離を表している。この慣性系を dx' = dy' = dz' = 0 という慣性系にローレンツ変換した （つまり３次元空間では静止している）ときでも、(dτ)2 = (dw')2 （不変量）は残る 。このことから dτ は、まさしく３次元的運動とは無関係不変量であり、その慣性系の「固有時」と呼ばれる。
[A] の式を４次元時空間の速度（４元速度）が項に明示できるように書き換えてみる。
1 = (dw/dτ)2 - (dx/dτ)2 - (dy/dτ)2 - (dz/dτ)2 [B]
これは (dτ)2 で[A]式を割っただけである。[B] 式右辺の各項は 各速度成分の２乗らしく見える。ところがそれは dτ という（dt によく似た）記号と固有時という言葉に騙されているのであって、[A]式を見れば dτ は距離であり各項は無単位の２乗。本当に速度の２乗にするには、[A] の両辺に光速の自乗 c2 を掛ければよい。
E = mc2 の立体アート（ベルリン） c2 = (cdw/dτ)2 - (cdx/dτ)2 - (cdy/dτ)2 - (cdz/dτ)2 [C]
今度は、[A]式を (cdt)2 で割ると、
(dτ/cdt)2 = 1 - 1/c2((dx/dt)2- (dy/dt)2 - (dz/dt)2) = 1 - v2/c2 = 1/(γ2)
となるので、cdt/dτ = γ （ローレンツ因子）である。したがって、
cdw/dτ = c（cdt/dτ) = cγ
cdx/dτ = (cdx/cdt)(cdt/dτ) = (dx/dt)γ = vxγ
cdy/dτ = vyγ
cdz/dτ = vzγ
以上が４元速度の各成分である。[C] を書き直すと、
c2 = (cγ)2 - (vxγ)2 - (vyγ)2 - (vzγ)2 [D]
右辺の各項は４元速度の成分の２乗である。[D]の両辺に m2 （m は質量）を掛けると、
(mc)2 = (mcy)2 - ((mvxγ)2 + (mvyγ)2 + (mvzγ)2) [E]
右辺の各項は運動量の２乗になる。
(mc)2 = (pw)2 - (px2 + py2 + pz2) = (pw)2 + p2 [E']
pw を求めると、pw =((mc)2 + p2)1/2 = mc (1+ p2/(mc)2)1/2 = mc + (1/2)p2/mc + … （マクローリン展開式）
cpw ≈ mc2 +(1/2)p2/m
第２項目は、本文①式の第１項の運動エネルギーと同じ形になることを見て、アインシュタインはこの cpw は全エネルギー E を表すと解釈したらしい。
E ≈ mc2 + (1/2)p2/m [F]
は運動エネルギーを無視すれば有名な E = mc2 （静止エネルギー）の公式となる。特殊相対性理論の最後の柱である。
[F] 式は近似式なので、
E2=(pc)2 + (mc2)2
が特殊相対性理論でのエネルギーと運動量の関係式を正確に表す（本文ではベクトル表現を省いた）。[E] と[E'] を比較すると、
p = mvγ。
これを使って変形し、
E = γmc2 = mc2(1 - v2/c2)1/2
という式もよく見かける。
2e/3
-e/3
e-
g
μ-
γ
τ-
W+ 
