日経平均とTOPIX終値を０７年1月から７年半分を周波数解析してみた。GPIFは株式を増やすべきではない！！

景気の良い人は，年金積立金のポートフォリオを見直して，株式および外国資産を増やすべきだと大声をだしているのだが，私は反対である。

で，根拠はないかと思って，日経平均とTOPIXの終値データを探してみた。引用元【【TOPIX】株価指数 時系列データ 日足】。

まずは，生データである。

２００７年1月４日～２０１４年６月６日までの日経平均とTOPIX終値の時系列データである。





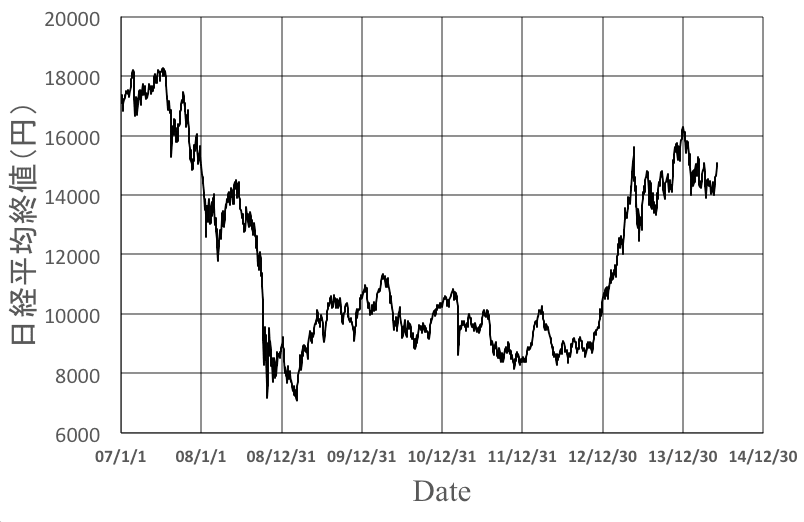
原データは，１８２０日分しかないため，FFTを実施するのは，１０２４データか２０４８データにしないとならない。できれば，周波数分解能を高めたいので，２０４８データにするために，未来のデータは，１８２０日分の平均値を並べた。土日祝日の市場が休みの日は無視して，１８２０日間連続データと考えた。

これをエクセルでFFTかけて，リニアスペクトラムを計算した結果が下のグラフ。FFTの解析条件は，サンプリング周期が1日，データ長2048，データウインドーが矩形。平均値のDCドリフトは，周波数０Hzに押し込んである。





このグラフの横軸は，周期（周波数の逆数）になっている。縦軸は，日経平均とTOPIX変動幅である。一般に周波数解析では，横軸は周波数となるが，今回の解析結果では，横軸を周期とした方が理解し易い。

同じ結果を期間中の平均値に対する変動をパーセント表示として，かつ，両対数軸にプロットすると，下のグラフになる。





この両対数軸のグラフの方が，日経平均とTOPIXの値幅変動と周期の関係を見る上では理解し易い。一般に，電気信号の周波数解析を行うと，周期の短い（周波数が高い）ほど，変動＝ノイズが大きくなる。しかし，TOPIXは長い周期の変動が大きい。株式投資において，リスクとは，期待値に対する変動の幅が大きいことがリスクとなる（一般に株価が下がることとがリスクとされるが，購入しようとする時は，値段が高いことがリスクとなる）。

簡単に言うと，２００７年1月４日～２０１４年６月６日までのTOPIXは，長く株式を持っていればいるほど，株価変動が大きいということを表している。つまり，リスクが大きいと言うことである。７年半保有では，約１０％程度の変動を許容する必要がある。

かつて，株価は，長期保有するほど有利であると言われた。それは，経済成長に伴い，株価も上昇するからだという理屈である。

しかし，ここ７年半だけを切り取ってみれば，長期で持つほど，値幅変動を大きく受けたと言う結果になっている。

株価は，人為的に変化するため，将来のリターンは確実ではない。となると，リスクを最少限にするためには，短気の売り買いをする必要があるが，そんなことを，安定運用を基本とする年金積立金でおこなうのであろうか？と，言う疑問がどうしても消すことが出来ない。

もっと，長期のデータで解析をすれば，より傾向は顕著になるであろうと思う。

株価のニュースが，常に，前日比や，年初来高値・安値の短気でしか報道されないことは，株式を仕事にしいている人たちは，短気の値動きににしか関心がないことのあらわれであろうと思う。

今の政府は，間違った方向に進んでいると考える。