自然界においてひも理論を実現できそうないくつもの方法を理解しようとしたら、もっと一般的な解を知る必要がある。
ひも理論のすべての解を理解することが重要だが、カラビ=ヤウ空間にはそれらすべては含まれない。
リー=シュン・ツェンは、カラビ=ヤウ多様体を円に喩えている。
描くことのできるすべての滑らかで閉じた一次元曲線のなかで、円はもっとも美しく特別だ。
ストロミンガー方程式には、カラビ=ヤウ条件を緩和することが関係しており、それは、円の条件を楕円の条件に緩和することに似ている。
一定の長さの閉じたひものループがあれば、つくることのできる円は一種類だけだが、その円をさまざまな程度で潰したり引き伸ばしたりすることで、限りない種類の楕円をつくることができる。
円は、そのループからつくることのできるすべての曲線の中で、中心周りの回転に関して不変である唯一のものだ。
楕円は円よりも少し複雑な系であり、同様に、ストロミンガーの(非ケーラー多様体)系は、より少ないパラメータで記述できるカラビ=ヤウよりも扱いが複雑だ。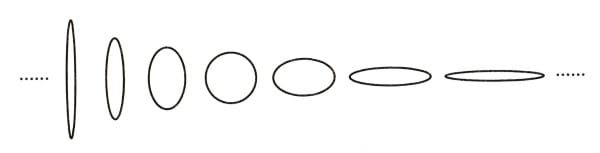
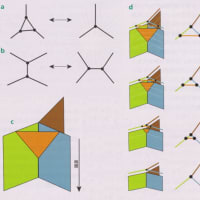
図4: 一定の長さのループがあれば,細長いものや丸いものなど無限種類の楕円をつくることができるが,その周長をもつ円は1つしかつくれない。つまり,円を特別なものにしている特性のいくつかを緩和すれば,どんな数の楕円でもつくれる。同様に,定義上ケーラー対称性をもつカラビ=ヤウ多様体は,もっと緩い条件を満たし,もっと幅広い種類の物体を含む非ケーラー多様体に比べ,はるかに特別だ(円のように)。
円から楕円へ、あるいはカラビ=ヤウ多様体から非ケーラー多様体へ変えると、対称性と美しさが一段階下がってしまうが、自然が必ずしも、もっとも対称的な構成を選ぶとは限らない。
たとえば惑星の楕円軌道を考えてほしい。
だから、私たちの自然の宇宙を記述する六次元内部幾何も、カラビ=ヤウほど対称的ではなく、ストロミンガーの系のようにそれより少し対称性が低いかもしれない。
ストロミンガーの提唱した系は、同時に解かなければならない四つの微分方程式の系から構成されており、しかもその一つ一つが悪夢のように難しいため、容易には取り扱えない。
一般相対論の内容を要約した有名なアインシュタイン方程式も、一つのテンソル方程式として書けるものの、やはり同じ理由で、実際には、物質とエネルギーの存在によって生じる時空の湾曲として重力を記述する、10個の場の方程式の組である。
カラビ予想の証明の際には、真空条件におけるアインシュタイン方程式を解くために、かなり厄介ではあったが、それをたった一つの方程式へ還元した。
非ケーラー多様体はカラビ=ヤウ多様体より扱いが難しいが、それは、対称性が低いために変数が多くなるからだ。
カラビ予想の場合は、ケーラー多様体を取り扱うために二世紀以上にわたって編み出されてきた代数幾何学の道具を用いたが、非ケーラー多様体の場合、それに相当するものは存在しないのだ。
それでも、数学的観点から見ればそれら二種類の多様体にそれほど違いはない。
カラビ=ヤウ多様体をつくる際には幾何解析が使われており、その手法は、もしストロミンガー方程式を解くことができる、あるいは少なくとも解が存在することを証明できれば、非ケーラー多様体をつくる上でも役に立つはずだ。
物理学者は、非ケーラー多様体が存在しうるかどうか、そして四つの方程式すべてを同時に満たせるかどうかを知る必要がある。
なぜなら、もしそれが不可能であれば、それに取り組むのは時間の無駄だからだ。
二〇〇四年に物理学者ジュン・リーとヤウが、ある種の非ケーラー多様体が数学的に存在可能であることを証明した。
つまり、知られているカラビ=ヤウ多様体それぞれについて、それと構造的に十分に似た一群の非ケーラー多様体が存在することを証明したのだ。
それは、非ケーラー多様体の存在が数学的に確認された初の例だった。
ストロミンガー方程式を解くのはとてつもなく難しいが、リーとヤウは、この分野において一番簡単にできることをやった。
つまり、非ケーラー多様体がカラビ=ヤウにきわめて近いという限られたケースにおいて、ストロミンガー方程式が解けることを証明したのだ。
具体的な方法としては、あるカラビ=ヤウ多様体からスタートし、その幾何、すなわち計量がケーラー的でなくなるところまでそれを変形させる。
その多様体は依然としてカラビ=ヤウ計量をもつことができるが、その計量はもはや非ケーラー的であり、ストロミンガーの系の解を与える。
おそらくはもっと重要なこととして、リーとヤウはDUY定理を一般化し、基本的にすべての非ケーラー多様体をカバーできるようにした。
DUYをものにできれば、四つのストロミンガー方程式のうち二つ - エルミート型ヤン=ミルズ理論に関連したもの - が自動的に満たされ、残りは超対称性とアノマリーのキャンセルの方程式を解くだけになるため、実用的に大きな価値がある。
カラビ=ヤウのコンパクト化においてDUYが役立ったことを考えると、非ケーラー多様体のコンパクト化にも同じことが期待できる。
ストロミンガー方程式は、非ケーラー多様体だけでなく、その特別なケースであるカラビ=ヤウ多様体にも当てはまるため、ここでも適切に使うことができそうに思われた。
またリードの予想には、カラビ=ヤウ多様体から非ケーラー多様体へ、あるいはその道へ移る手順が含まれている。
そこで、それらの幾何の両方をカバーできる方程式が必要だとしたら、ストロミンガーの方程式がまさにそれにぴったりかもしれないと思った。
いまのところ、クレメンスの多様体が実際に四つのストロミンガー方程式のうち三つを満たすことまでは証明できている。
しかし、もっとも難しいアノマリーキャンセルの方程式の解は見つかっていない。
ヤウは「いまでも、その多様体が存在すると確信している。さまざまな人間の努力から見れば、四つのうち三つというのはかなりいい方だ。しかし最後の方程式を解くまでは、何も証明したことにはならない」という。
フーとヤウはさらに別の例を使い、ストロミンガー方程式を満たす、トポロジー的に多様な種類の非ケーラー多様体を構築する方法を示した。
それらの多様体は、既知のカラビ=ヤウ多様体を変形させてつくるのではなく、ゼロから組み立てるため、もとから非ケーラー的だ。
それらは、すべての点に二次元トーラスをくっつけたK3曲面(四次元カラビ=ヤウ多様体)からなる。
この場合、ストロミンガー方程式を解くには、かつてのカラビ予想の証明のときよりも複雑なモンジュ=アンペール方程式を解かなければならなかった。
幸いにも、以前の論証をもとにその証明を組み立てることができた。
二人は、一つだけでなく四つの方程式をすべて解けるようにする特別な方法を発見した。
カラビ予想の場合にはモンジュ=アンペール方程式の可能な解をすべて求めることができたが、このときは可能な解の部分集合しか得られなかった。
残念なことに、この系についてはあまりよく理解できておらず、その部分集合がどれだけ大きいか小さいかはわかっていない。
少なくとも、予備的な段階をいくつか進むことはできた。
非ケーラー多様体のコンパクト化に取り組みはじめた物理学者のほとんどは、わざわざ証明しなくてもストロミンガー方程式を解くことはできると考えている。
リー、フー、ヤウは、これまでに特定した個別のアプローチにおいてストロミンガー方程式を解けることを証明しており、それらの特定の多様体 - 非ケーラー多様体全体のうちの一部 - が実際に存在することはわかっている。
すなわち、ストロミンガーの系とそのすべての方程式を、もっとも一般的な形で満たす計量を見つけるという問題だ。
まだ誰もその目標に近づいてはおらず、あらゆる証拠からその証明は決して簡単ではないと思われるが、もっとささやかなステップとして、少なくともその可能性を引き上げた。ヤウは、「カラビ予想を証明するまで、その重要性に完全には気づいていなかった。証明してからでさえ、物理学者がその証明とそれに伴う定理の重要性を認めるまでに八年かかった。それでもカラビ=ヤウ空間の探究を続けたのは、それが美しく見えたからだ。ストロミンガーの系によって特徴づけられる空間も、かなりの魅力をもっている。どのような展開になるか見守っていく必要があるだろう」という。
現在、調べられている非ケーラー多様体のコンパクト化や、その他多くのカラビ=ヤウ多様体の代替物を使って進められている取り組みから何が出てくるか、正確に言うのは難しい。
カラビ=ヤウ多様体のコンパクト化が私たちの宇宙の正しい記述なのか、それとも単に、これまで見いだしてきた中でももっとも単純な例、すなわち、ひも理論のしくみ、および超対称性やすべての力など「究極の理論」に必要な要素の求め方を知るための思考実験にすぎないのか、それはわからない。
いまのところ私たちは、ひも理論のランドスケープに広がる数多くの可能性のうちいくつかを調べようとしているにすぎない。
しかし、それらの膨大な可能性の中にあるたった一つの宇宙に私たちは住んでおり、その宇宙はやはりカラビ=ヤウ幾何によって定義できるかもしれない。
最新の画像[もっと見る]
-
 タイムトラベルとタイムマシン?
10年前
タイムトラベルとタイムマシン?
10年前
-
 パウリの夢の数式に「虚数」が生み出された!
10年前
パウリの夢の数式に「虚数」が生み出された!
10年前
-
 「微細構造定数」137とパウリ&ユング
10年前
「微細構造定数」137とパウリ&ユング
10年前
-
 宇宙インフレーション 超弦理論
11年前
宇宙インフレーション 超弦理論
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 拡張標準モデルとは?
11年前
拡張標準モデルとは?
11年前
-
 相対性理論とローレンツ対称性
11年前
相対性理論とローレンツ対称性
11年前
-
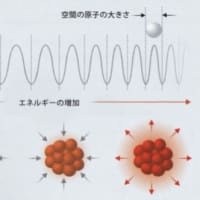
 宇宙の起源に新説か?
11年前
宇宙の起源に新説か?
11年前
-
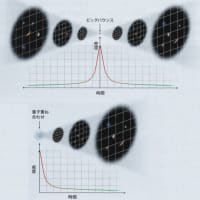
 宇宙の始まりは「ビッグバウンス」?
11年前
宇宙の始まりは「ビッグバウンス」?
11年前
-
 「スピンの泡」が時空に対応する、ループ量子重力
11年前
「スピンの泡」が時空に対応する、ループ量子重力
11年前










※コメント投稿者のブログIDはブログ作成者のみに通知されます