フィボナッチの数列をExcelで作ろうとしてみる

　先日　黄金比について面白い話を伺いました。

　「黄金比は、バランスのとれた美しい構成比として古くから洋の東西を問わず知られていたもので、エンシャント・グリークでパルテノン神殿のファーサイトとか、興福寺の阿修羅像など沢山使われているものです。これがフィボナッチの数列に関係があります」

　え、フィボナッチの数列ですか。
大事なものらしいですけれど、なにしろ小学校で算数をあきらめたものですから苦手なんですよ。
思いつくのは、吉田秋生さんの漫画くらいです。

別冊少女コミックに連載された「BANANA FISH」で、天才不良少年アッシュ・リンクスが知能テストを受けたとき使っていますね。

　とりあえずつくってみますか。Excelで簡単にできるでしょう。
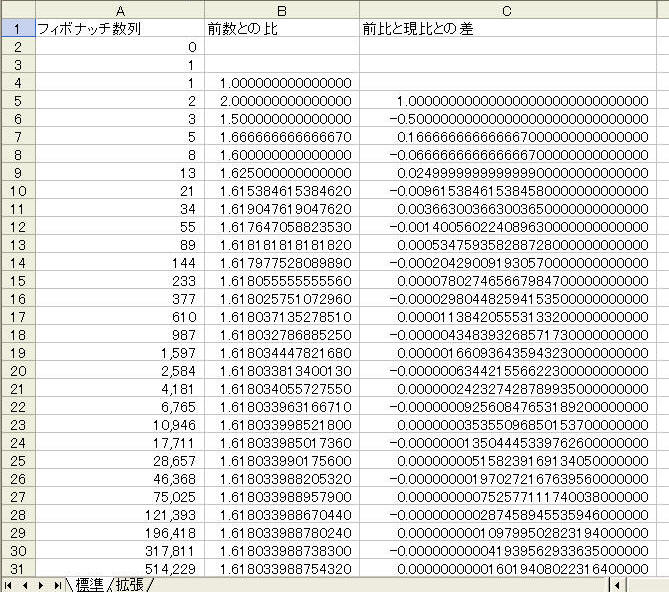
最初は０　次は１を　その次の数は前とその前を足したもの（以後つづく）
なので第３項目は　＝SUM(A2+A3)
あとはオートフィルで下まで下げて、はいできました。
　出来た数を、その前の数で割ると面白い結果になるんですね。
やってみましょう。
B4のセルに＝PRODUCT(A4/A3)と入れましてまたオートフィルで下まで。
はいできました。
４２行目の１０２，３３４，１５５から下は１．６１８０３３９８８７４９８９０だけです。
これって、黄金比の近似値ですよね。凄いな





　ちょっと待ってね、比が決まるのはおかしくないですか？
求めたものは整数を別の整数で割ったもので、分数ですから有理数でしょう。
無理数である黄金比そのものになるはずないですね。
どこまでも黄金比に近づいている最中というわけではないのかな。
もう少し下まで見てみましょう。



　７６行目　下一桁は７のはずですが０です。
Excelにバグがあるのか？というほど大げさなものではなく、
Excelは有効桁数１５桁なので１６桁目は意味が無いということですね。
前数との比が「４２行目の１０２，３３４，１５５から下は１．６１８０３３９８８７４９８９０だけです」というのは、これ以降は末尾の数字は意味が無くなったというだけなのですね。
うっかりしていたけれど７行目は６が続く循環小数のはずですよね。ここで気づくべきでしたね。
やっぱり算数は苦手だな。

　前の比と今の比の差を求めてみると、どんどん差が小さくなってきていますね。
Excelが計算しなくなった後も、値は黄金比に収斂していっているのでしょうね。
行き着くことはないはずですが。

　こういうのはもっと高級言語で計算するものなのでしょうね。


　せっかくなので遊んでみましょう。
１項目と２項目が大きく違っていても、その比は黄金比にむかって収斂していくのでしょうか？
１の代わりに今日の日付けから２０１００６１８と入れてみましょう。


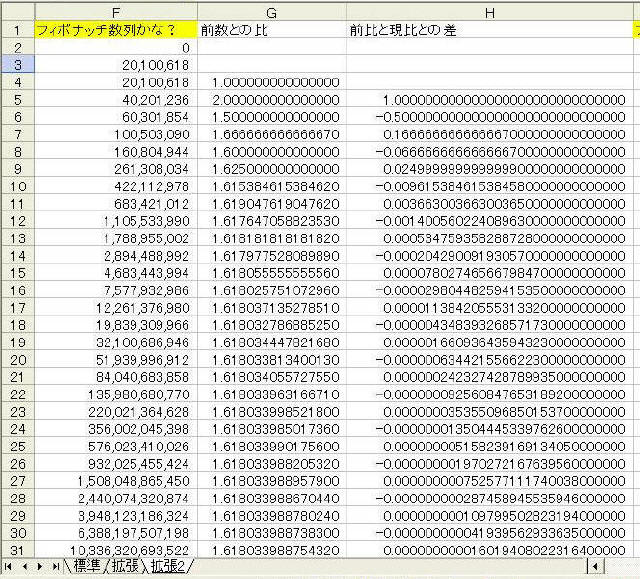
　どんな数でも「前の数を足して次の数をつくる」という手順を繰り返すと、いずれは前項との比は黄金比の近似値になるらしいですね。
まってよ、まだ正の整数つまり自然数しか考えていないですね。

　０はどうでしょう。
０に０を足してもまたそれを０で割っても意味があるとは言えませんね。
　負の数ではどうでしょう。
ただマイナスが付くだけで成立していますね。
　整数でなければどうでしょう。
たとえば循環小数である１/７を入力してみましょう。
例によりExcelでは１５桁までしか計算しませんが、だいたい成り立っているみたいですね。
そうすると、近似値を小数であらわせるような数はだいたい成り立つのでしょうね。
円周率とか３の平方根など無理数でも同様でしょう。

　つまり０以外の実数では成り立つらしいのでしょうね。



　複素数については分かりませんね。
（横軸に実数座標、縦軸に虚数座標の）複素平面でヴィジュアルにあらわされるのでなんか解ったような気になりますが、複素平面とは「横軸の単位はメートルだけど、縦軸の単位はわかりません。ミリなのかなキロなのかな、オングストロームかな、パーセクかな」というようなもので理解を超えています。

　０を除く実数は「前の数を足して次の数をつくる」という手順を繰り返すと、いずれは前項との比は黄金比の近似値になるらしい　　くらいが想像できるところですね。

　あれ　よく見ると、これらはフィボナッチの数列に定数を掛けただけか。成り立って当たり前か。




　考えを発展させて、始めの数を０と限らないとします。

　（いずれではなくて、すぐに）どの数からでも前項との比が黄金比の近似値である（前項を足すと次項になる）数列があるのじゃないのかな。
３行目に＝INT(上のセル＊１．６１８０３３９８８７４９８９）と入れます。
（これは整数に限りたい場合です。一般的にはSUMでしょう）
上のセルに２０１００６１８と入れます。



　凄いね。

任意の実数からはじまる、前項との比が黄金比に近づいていく数列を簡単につくれる　ということですね。

　今度は別に、最初の数と次の数を適当に入れてみましょう。



　面白い。フィボナッチの数列でなくても、いずれは黄金比に近づいていきます。

　今　学生だったとしたら、
「初項と次項の組み合わせごとの、黄金比の近似値に収斂するまでの揺らぎ」を足がかりに、
数論に挑みたくなるような気がしますね。
これって楽しいもの。

　数論というものは天才がやるものなので、手におえないでしょうけれど。