コンデンサの繋ぎ換え

知恵袋：https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12293051302

 

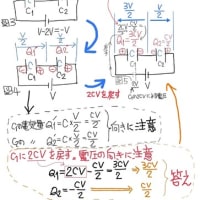
▶↑は保存則での解法

▶別解

（C1,C2は直列、電荷を等価電圧へ置換えて解く方法）

C1の静電容量C1=1.0μF
C2の静電容量C2=2.0μF
みたいですのでC1の始めの電圧V1=30μC/1.0μF=30V、↑向きの電圧

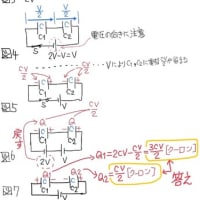
なので図bの様に繋ぐとC1,C2に新たに追加される電荷量Q'は
（公式 Q=CVで使う電圧Vは
等価電源の電圧Vとして
V=12.0−(C1の電圧V1=30[V])=12.0−30=−18.0[V]

この18.0[V]がマイナスと云う事は等価電源は↓向きの電圧と云う事です。この↓向きと云う電圧の向きを覚えておいてください）

故に
Q'=(C1,C2の直列の合成容量)×(−18.0V)
=1/(1/1.0+1/2.0)×18.0
=2.0/3×18
=2.0×6
=12.0μC（↓向きの電圧）

この電荷量Q'が図bのC1,C2に溜まるのですが、C1には予め30μCの電荷（↑向きの電圧）があったので、
図bにおけるC1,C2の各電荷量Q,Q'は

Q=30−Q'=30−12.0=18.0μC、↑向きの電圧18.0[V]
Q'=12.0μC、↓向きの電圧6.0[V]

なのでC2の電圧は↓向きの電圧なので
TはSよりも電位が6.0[v]高い
と云う事です。