Excelでローン返済をシミュレーションしてみる。 シミュレーション・サイトがあるので、自分で作る必要はないと思われるだろう。 しかし、Excelの使い方を習得するには良い教材なので、チャレンジしてみるとよい。
住宅や車をローンで購入する計画があれば、このシミュレーションでローンについて理解を深めておくと良い。 同様にExcelで返済表を作ると、残高の減少具合がよくわかる。特に残高をグラフ化すると金利というものを実感できる。
私は、住宅ローンを10年間返済した時点で借り替えをした。 その時、銀行員はプリントされた表を元に毎月の返済額を電卓で計算していた。 こちらは事前にPCでシミュレーションしてある。 その結果を見て、「ほぼ合ってますね。 正式な返済額はコンピュータで計算し、返済表を後日郵送します」と言う。 なにしろ、10数年も前のことで、銀行窓口にPCなど無かった時代。 応対した銀行員は「やり難い客だ」と思っただろう。
■元利均等返済(金利は固定)のシミュレーション
一般的なローン返済に「元利均等返済」がある。 毎回の返済を一定金額で行うもの。 この返済額をシミュレーションする。
借入元金をA円、年利がR%、返済年数がN年の場合
A×r×P
毎月の返済額 = ----------------
(P-1)
ここで、r(月利): 月当たりの利息(=R÷1200)
年利を月利にするために12で割り、さらに%表示値を少数値にするために100で割る
n(返済回数): 返済期間中の月数(=N×12)
P: 計算上の中間値で(1+r)をn剰したもの
■Excelに組み込む
下図のように、セルB3~B5には「借入元金 A」、「年利 R」、「返済年数 N」と書き込む。セルC3~C5にはシミュレーション時に数値を入力。
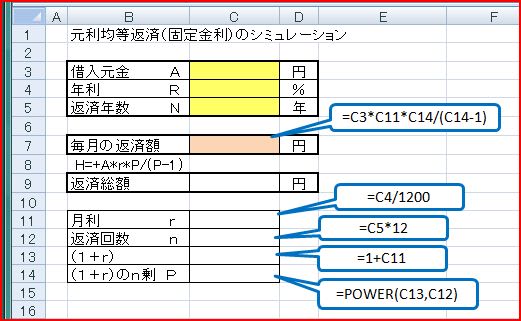
セルB7には「毎月の返済額」と入力し、セルC7にシミュレーション結果が表示されるように計算式を入力する。 ここでは計算式をわかり易くするために、中間値としてr、n、(1+r)などを先に求めておき、セルC7で最終計算を行う。
これら中間値およびシミュレーション結果を求める式は図中にフウセンで示してある。 なお、計算では利率は%値ではなく小数値で行われることに注意。
セルC14で使用するPOWER関数について説明しよう。 POWER(A,N)はAをN乗、つまりN回掛け合わすもので、C14に入力するPOWER関数は、セルC13の値をセルC12の値分だけ掛け合わすことを意味している。 以上でシミュレーション準備が完了。
■具体的な数字を入れてシミュレーション
借入元金を10,000,000円、年利3.40%、返済年数を20年とした場合、毎月の返済額は57,483円という結果が出る(下図)。

ボーナス併用の場合は、月返済と同様にボーナス返済分を計算して両者を加算すればよい。 ボーナス返済は年2回返済なので、月利ではなく半年利率を用い、返済回数は返済年数の2倍となる。
◇この続きは、Excelで返済表を作る
住宅や車をローンで購入する計画があれば、このシミュレーションでローンについて理解を深めておくと良い。 同様にExcelで返済表を作ると、残高の減少具合がよくわかる。特に残高をグラフ化すると金利というものを実感できる。
私は、住宅ローンを10年間返済した時点で借り替えをした。 その時、銀行員はプリントされた表を元に毎月の返済額を電卓で計算していた。 こちらは事前にPCでシミュレーションしてある。 その結果を見て、「ほぼ合ってますね。 正式な返済額はコンピュータで計算し、返済表を後日郵送します」と言う。 なにしろ、10数年も前のことで、銀行窓口にPCなど無かった時代。 応対した銀行員は「やり難い客だ」と思っただろう。
■元利均等返済(金利は固定)のシミュレーション
一般的なローン返済に「元利均等返済」がある。 毎回の返済を一定金額で行うもの。 この返済額をシミュレーションする。
借入元金をA円、年利がR%、返済年数がN年の場合
A×r×P
毎月の返済額 = ----------------
(P-1)
ここで、r(月利): 月当たりの利息(=R÷1200)
年利を月利にするために12で割り、さらに%表示値を少数値にするために100で割る
n(返済回数): 返済期間中の月数(=N×12)
P: 計算上の中間値で(1+r)をn剰したもの
■Excelに組み込む
下図のように、セルB3~B5には「借入元金 A」、「年利 R」、「返済年数 N」と書き込む。セルC3~C5にはシミュレーション時に数値を入力。

セルB7には「毎月の返済額」と入力し、セルC7にシミュレーション結果が表示されるように計算式を入力する。 ここでは計算式をわかり易くするために、中間値としてr、n、(1+r)などを先に求めておき、セルC7で最終計算を行う。
これら中間値およびシミュレーション結果を求める式は図中にフウセンで示してある。 なお、計算では利率は%値ではなく小数値で行われることに注意。
セルC14で使用するPOWER関数について説明しよう。 POWER(A,N)はAをN乗、つまりN回掛け合わすもので、C14に入力するPOWER関数は、セルC13の値をセルC12の値分だけ掛け合わすことを意味している。 以上でシミュレーション準備が完了。
■具体的な数字を入れてシミュレーション
借入元金を10,000,000円、年利3.40%、返済年数を20年とした場合、毎月の返済額は57,483円という結果が出る(下図)。

ボーナス併用の場合は、月返済と同様にボーナス返済分を計算して両者を加算すればよい。 ボーナス返済は年2回返済なので、月利ではなく半年利率を用い、返済回数は返済年数の2倍となる。
◇この続きは、Excelで返済表を作る