Example Oriented Learning

{Example Oriented Learning}/HCU?
@http://blog.goo.ne.jp/ep58-kit/e/9f6ddc9f714324c2e586e5f021db5d9e

---

%0:Example Oriented Learning

・公式の丸暗記を避けるための一つの方法は，公式になる直前の式（以下，仕掛品といいます）を覚えることです．

{丸暗記による公式の誤用例}
@http://blog.goo.ne.jp/bonsai-chat/e/bce61d58f8dda8c6717a90bb646369a5

"Example Oriented Learning" emphasizes that refined examples are better than
generalized explanation with formulas and theorems in education.

%1:Simple Examples

%1.0:Example1.0
Let  f(x)=x²+2x+3=0.  Then
  x²+2x+1-4=0.
  (x+1)²=4.
Hence
  x+1=±2

%1.1:Example1.1
Let  f(x)=ax²+bx+c=0(a≠0).  Then
a(x+b/2a)²+c/a-b²/4a
a(x+b/2a)²+c/a-b²/4ac
a(x+b/2a)²=b²-4ac/2a
x=(-b)±(b²-4ac)^1/2)/2a
・usually, 「(b²-4ac)^1/2」is expressed in anotherway.

%1.2:Example1.2
If f(x)=x²+2x+3=0, Then f(1)=1+2+3=0.
f(x)/(x-1)=x+3,f(x)=(x-1)(x+3)


%2:Difficult Examples

%2.1:Example2.1

When f(x)=x²+2x+5=0,
  (x+1)²=-4.
Suppose that there exists the number  i such that i²=-1,
  x+1=±2i
・Imaginary unit「i」is a difficult number
explained in [B2014-03.pdf] 
https://researchmap.jp/?page_id=398&lang=english
2014/03/01　GF(3) の拡大　研究ブログ
can be downloaded from
https://1drv.ms/b/s!Ahb2teuYQIZ7hV1Zg4CDqSkeRlo6
・「GF(3)」is better example than 「GF(3)」to unerstand the properties of「GF(pⁿ)」.

%2.2:Kirchhoff's Law

There exist students who cannot use Kirchhoff's Law, and give up to solve simple problems like

https://eleking.net/k21/k21t/k21t-combined.html

・Examples in [%0].{公式より仕掛品} cannot be solved without understanding Kirchhoff's Law

%2.3:Heaviside Operator

https://en.wikipedia.org/wiki/Operational_calculus

At the time, Heaviside's methods were not rigorous, and his work was not further developed by mathematicians.
This technique was fully developed by the physicist Oliver Heaviside in 1893.

%2.4:・How to Solve It
https://en.wikipedia.org/wiki/How_to_Solve_It

%4:Inadequate Examples in {例題指向型教材}

%4.1:Example
NaOH+2HCl →？
http://www.nhk.or.jp/kokokoza/tv/kagakukiso/archive/resume031.html

%42:嘘つきのパラドックス
https://ja.wikipedia.org/wiki/自己言及のパラドックス
https://en.wikipedia.org/wiki/Liar_paradox
For a better understanding of the liar paradox, it is useful to write it down in a more formal way. If "this statement is false" is denoted by A and its truth value is being sought, it is necessary to find a condition that restricts the choice of possible truth values of A. Because A is self-referential it is possible to give the condition by an equation.

---

%5:How to Select examples

%5.1:[?HCD:減加法の筆算]への補足

---

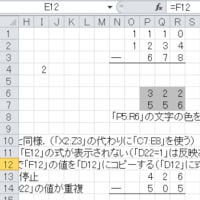
Procedure is shown using representative column 「Q」

・Probably, such explanation is much easier to read than that of
exact translation of the original sentence

---

 ={List of Files}

---