タクシー数(その5)

 だんだん、本来のタクシー数からは離れて行くが、その4に引き続き、2次体の整数を用いてn乗数の和で2通りに表される例を考えてみる。

 

  先ず、その4で対象としたの形の数の計算を行ってみる。最初は簡単な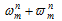について、nの偶奇に応じて計算を行う。

 

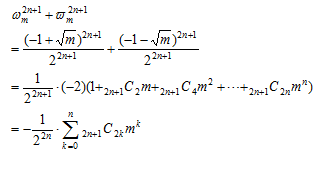
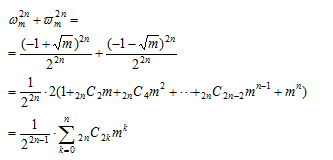
 次にについて、同じくnの偶奇に応じて計算を行う。

 

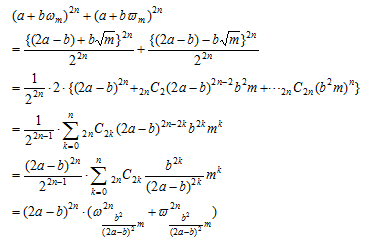
 となる。

簡単とするため　b＝1かつ奇数乗の場合を考えると

 

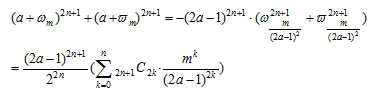
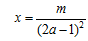とおき、これをa,x,mの関数F(a,x,n)と考えると

 

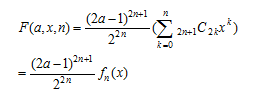
今、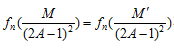なる整数A,M,M’が存在すれば

 

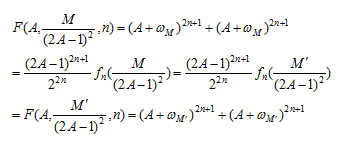
となり、2通りに2次体の整数により(2n+1）乗数の和としてあらわされる。

 

小さなnについて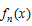を求めると

 

である。簡単な計算で

 

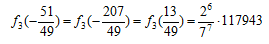
したがって、

 

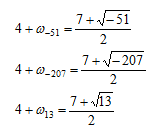
より

 

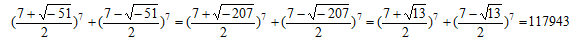
また、

 

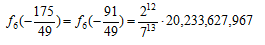
したがって、

 

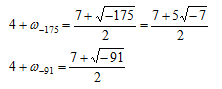
より

 

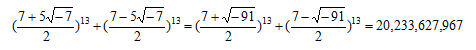
すべての奇数乗について、このような解があるのだろうか。