メモ8と9で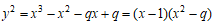 
q≠0,1の非負整数
の位数∞の整数解について考えた。q=38089のときCoCalcでgens()により生成元を求めると、以下4つの整数解が得られる。
P1=(-195,112)
P2=(-183,920)
P3=(-161,1404)
P4=(-91,1656)
また、ねじれ元は 位数2の Q=(1,0) のみである。
これらのP1,P2,P3,P4 及びQは、この楕円曲線の有理点群の生成を保証しているのだろうか？
これまでそう考えてきたが、CoCalcのマニュアルの gens の説明によると
Contrary to what the name of this method suggests, the points it returns do not always generate a subgroup of full rank in the Mordell-Weil group, nor are they necessarily linearly independent. Moreover, the number of points can be smaller or larger than what one could expect after calling rank()or rank_bounds().
(出典:http://doc.sagemath.org/html/en/reference/curves/sage/schemes/elliptic_curves/ell_number_field.html)
とあり、有理点群の生成どころか、フルランクの部分群の生成も保証していないし、得られたこれらの有理点の独立性も保証していない。
では、与えられた有理点が独立かどうかはどう判断すればよいだろうか？
Q上の楕円曲線の有理点の独立性について、WEB上の論文などをみると、次のようなことが書かれている。(例えば、Elliptic curves with high rank, MICHEL ARTHUR BIK, Technische Universiteit Delft, 2014)
・Q上の楕円曲線 
の有理点P=(x,y) x=p/q gcd(p,q)=1 について、 高さ関数 h:E(Q) → R を h(P)=log(max{|p|,|q|}) で定義するとき、
n → ∞ のとき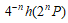 
は収束する
・
とし、 ペアリング <・,・>：E(Q)×E(Q) → R を
と定義するとき、ペアリング <・,・> はE(Q)上で双一次形式である。
・P1,・・・・・,Pm ∈ E(Q)に対し、行列 
が逆行列を持てば、P1,・・・・・,Pmは一次独立である。
これをそのまま適用するのも大変そうなので、もっと簡単に有理点の独立性が確認できないか考えてみた。
メモ5(楕円曲線のランクの計算例)にSilvermanとTateによる”Rational Points of Elliptic Curve”(1994年第2版。 以下、[Sil]と記述する。)に紹介されているランクの計算法を記した。そこで記したφ、ψ、αなどの性質を利用して、冒頭に紹介した楕円曲線の有理点が一次独立であること、したがってランクは４以上であることを以下に示したい。
命題１：CとC'を以下で与えられる整数係数の楕円曲線とする
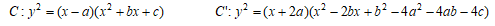
T=(a,0), T'=(-2a,0) とし、O, O'をC,C'の有理点群C(Q), C'(Q)の零元とするとき
(a) 以下で定義される準同型 ψ：C’ → C があり、その核は｛O’, T’}である。
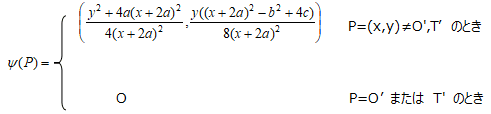
(b) (a)と同じプロセスをC’に施すと、ψ’：C’’ → C' があり、C''は(x,y)→(x/4,y/8)によりCと 同型である。したがって、以下で定義される準同型 φ：C → C’がある。
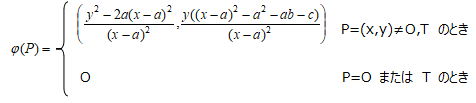
また、 
は2倍写像である。
【説明】：これはメモ5(楕円曲線のランクの計算例)で紹介した[Sil]のP79にある命題を3次式の定数が0でない場合に書き変えたものに過ぎない。つまりa=0とすればP79の命題が得られる。
C上の点のP=(x,y)に対し、
とおくと
である。ここで 
とおくと
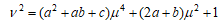
である。この式を本ブログの「4次楕円曲線」で紹介した方法でWeierstrass標準形に直すと
に注意すると
となり、（X,Y)と(μ、ν)の関係は
で与えられる。したがって、
これより
(ｙ＝－ABかもしれないが、その時は-yをyとすればよい)
ここで X'=X+b とおくと
となる。また、X' と Y の関係は
である。したがって C' の有理点 (X', Y) から C の有理点 (x, y) への有理写像
が定義される。あとは、これが準同型であることを示せばよいが、
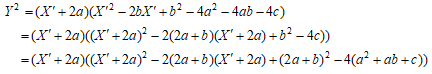
であることに注意すれば ψ は
と分解される。
ここで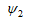 
は
としたときの、「Sil]P79のψ、同じことであるがメモ5の命題1のψに相当する。
また、
より、
が Cへの写像であることが分かる。また、
はy軸を平行移動させただけであるので準同型である。したがって、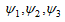
の合成であるψも準同型である。これで(a)が示された。
(b)については、
とおくとき
より (a)を楕円曲線C'と 
に適用して、以下に示す準同型ψ’’：C’’→C'が得られる。
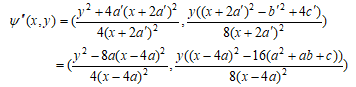
C''上の点(x,y)について
より、(x,y)→（4x,8y) によりCはC''と同型である。よって、この写像をψ''と合成して
を得る。
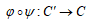及び 
が2倍写像であることは、上記、φとψの組み立て方から[Sil]のP79の命題の結果を用いて得られる。 【説明終】
命題2： Cと C'を以下で与えられる整数係数の楕円曲線とする。
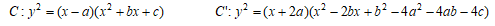
また、C(Q),C’(Q)をそれぞれC,C'の有理点のなすアーベル群、ψを命題1に記したC'→Cの準同型とする。このとき、以下の完全系列が得られる。
ここで、αは以下で定義される準同型である。
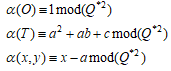
【説明】: ψは準同型なのでψ(C'(Q))はC(Q)の部分群である。したがって、ψ(C'(Q))＝ker(α) であることを言えばよい。
命題1のψの式より ψ(C'(Q)) ⊂ ker(α) はよい。また、α(x,y) ∈ ker(α) であれば
とかけるので、命題1の説明より α(x,y) ∈ ψ(C'(Q)) がわかる。 【説明終】
命題3: Cを以下で与えられる整数係数の楕円曲線とする。
C(Q)をCの有理点のなすアーベル群、αを命題2に記した準同型とする。また、C(Q)がねじれ元は位数2の元Tのみであるとする。このとき、
位数∞のの有理点Pi, Pj ∈ C(Q) に対し、α(Pi)≠α(Pj)かつ1に等しくないならば、PiとPjは独立
【説明】: mPi+nPj=0とする。
かつ 
なので
m,nともに偶数である。したがって、2(ｍ/2*Pi+n/2*Pj)=0 よって、C(Q)の唯一の位数2の元をTとすれば、ｍ/2*Pi+n/2*Pj=0 または T である。
このとき、ｍ/2*Pi+n/2*Pj=T とすると m/2またはn/2は奇数としてよい。双方ともに偶数とすると
ｍ/2*Pi+n/2*Pj=2(ｍ/4*Pi+n/4*Pj)=T となり ｍ/4*Pi+n/4*Pjは位数4の元となり矛盾。
したがって、ｍ/2*Pi+n/2*Pj=0 となる。
これより、m,nともに0でなければ、mPi+nPj=0 について最初から、ｍ、ｎのどちらかは奇数としてよい。今、nを奇数とすると、
m：偶数のとき、mPi+nPj=0 なので 
となり矛盾。
m:奇数のとき 
となり 矛盾。したがって、m=n=0である。 【説明終】
命題4：CとC'を命題2と同じ楕円曲線とする。また、C(Q),C’(Q)をそれぞれC,C'の有理点のなすアーベル群、ψを命題1に記したC'→Cの準同型とする。C(Q) のねじれ元は位数2の元T=(a,0)のみであるとする。GをC(Q)の部分群とするとき、以下が成り立つ。
(1) 
特にG=C(Q)とすれば 
したがって、
rはC(Q) のランク
(2) 
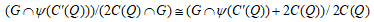
(3) 
(4) 
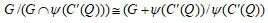
(5) 
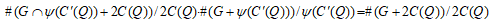
【説明】
(1) ψ(C'(Q))⊃2C(Q) に注意すれば準同型定理を適用すればよい。
G=C(Q)のとき C(Q)/２C(Q)は r+1 個のZ/2Zの直和になる。
(2) g,g' ∈ G∩ψ(C'(Q))について g≡g’ mod 2C(Q) であればg-g' ∈ ２C(Q)∩G
また G∩ψ(C'(Q))+2C(Q)の元 h は G∩ψ(C'(Q))の元 g により h≡g mod 2C(Q)
したがって、両者は同型
(3) (4)は(2)と同様
(5) (1),(2),(3),(4)よりすぐに得られる。 【説明終】
ここで冒頭の楕円曲線 C: 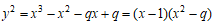q=38089 に戻る。
命題１、2の記号に従えば、a=1, b=0, c=-q=-38089 である。また、C'は
で定義される楕円曲線である。
よって、
において α(P1)=α(-195,112)=-195-1＝-196＝-14*14＝-1
α(P2)=α(-183,920)=-184-1=-2*2**2*23=-2*23
α(P3)=α(-161,1404)=-161-1=-2*9*9=-2
α(P4)=α(-91,16569=-91-1= -2*2*23=-23
α(T)=α(1,0)=(-38089)-1=-2*2*2*3*3*23*23=-2
これより、P1,P2,P3,P4は、命題3の仮定を満足することに注意する。
C'の有理点をCoCalcにより求めると、4つの位数無限大の整数解
R1=(0, 552), R2=(23, 1955), R3=(80, 3608), R4=(322, 9108)
と位数2のねじれ元 (-2，0) が得られる。
命題1より、C'の有理点(x,y)が零元及び(-2,0)でなければ、a=1, c=-38089 に注意すれば
R1,R2,R3,R4のψによる像と、その像のαによる像は以下のとおりであり、確かにψ(Ri)がαの核に含まれることがわかる。
ψ(R1)=(19045,-2628072) α(ψ(R1))=19044=138の2乗
ψ(R2)=(152981/100,-59326821/1000) α(ψ(R2))=152881/100=(391/10)の2乗
ψ(R3)=(485,-9768) α(ψ(R3))=464=22の2乗
ψ(R4)=(64333/324,-2996785/5832) α(ψ(R4))=64009/324=(253/18)の2乗
また、計算により
ψ(R1)=-P1-P2-P3+P4
ψ(R2)=2P2
Ψ(R3)=-2P2-P3+T
ψ(R4)=2P4
今、GをP1, P2, P3, P4で生成される群とする。P1, P2,P3,P4が線形独立であることを示すには、この群のrankが4であることをいえばよい。
まず 
について考える。
であるためには、k1、k2、k3とも偶数でなければならない。したがって、は8以上である。
次に 
について考える。
ψ(R1)=-P1-P2-P3+P4, Ψ(R3)=-2P2-P3+T, ψ(R1-R3)=P1-P2+P4+T が 2C(Q) に含まれない (＊)
とすれば、
TはGに含まれない。なぜなら、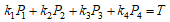
とすると、
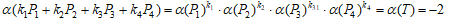
より、k1,k2,k4の偶奇が同一でk3とは偶奇が逆となる。
k1,k2,k4が偶数、k3が奇数のときは、P3-T∈2C(Q) これは仮定(＊)に矛盾
k1,k2,k4が奇数、k3が偶数のときは、-P1-P2+P4+T∈2C(Q) これも仮定(＊)に矛盾
は2以上、 は8以上なので
命題4(5)より、
は16より大きい。また、G+2C(Q)もTを含まない。仮に
g=
∈G, h∈2C(Q)についてg+2h=T とすると k1,k2,k4の偶奇が同一でk3とは偶奇が逆となる。
k1,k2,k4が偶数、k3が奇数のときは、P3-T∈2C(Q) これは仮定(＊)に矛盾
k1,k2,k4が奇数、k3が偶数のときは、-P1-P2+P4+T∈2C(Q) これも仮定(＊)に矛盾
よって、G+2C(Q)は自由アーベル群である。 は16より大きいのでG+2C(Q)のランクは4以上。Gのランクも4以上。
あとは、仮定(＊)を示せばよい。
命題5：
を有理数係数の楕円曲線とする。Cの有理点P= (x1,y1)について P=2RなるCの有理点R=(x,y)が存在するためには、
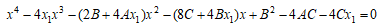が有理数解をもつことが必要十分である。
【説明】: 本プログのメモ4(楕円曲線の加法公式)より、2R のx1座標について
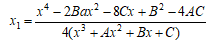
分母を払って、xの多項式として整理すると
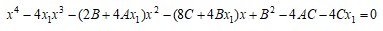【説明終】
また、楕円曲線 C: 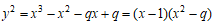q=38089 に戻る。
CoCalc により、計算すると
ψ(R1)=-P1-P2-P3+P4＝(19045,-2628072)
Ψ(R3)=-2P2-P3+T＝(485, -9768)
ψ(R1-R3)=P1-P2+P4+T＝(29341/100,3746439/1000)
これらに命題5を適用すると、A=-1, B=-q, C=q に注意し
x1=19045, 485, 29341/100 について
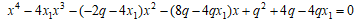
が有理数解をもたないことがいえれば仮定(＊)が成り立つ。CoCalcにより、これらの4次方程式は2次方程式の積に分解され、有理数解はないことがわかる。
以上でこのメモは終了であるが、最後に記したことは、ψ(C'(Q))の元が2C(Q)に含まれないことと上の4次方程式が2次方程式の積に分解することが同値であることを意味するのかもしれない。