楕円曲線にアーベル群の構造が入ることはよく知られており、加法の定め方も良く説明されているが、P=(x1,y1)とQ=(x2,y2)が楕円曲線上の点である時、P+Qの座標値をPとQの座標値から明示的に示す式は、演習問題としてよく出される。但し、具体的な式にはあまりお目にかかれないので、ここに書き留めておきたい。
Weiestrass 標準形
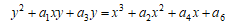
で考えると複雑になるりすぎると思われるので、a1=a3=0のケース、すなわち

で考えることとする。
楕円曲線上の原点でない2点をP=(x1,y1)とQ=(x2,y2)とする。
○ x1≠x2の場合
PとQを結ぶ直線の方程式は

とあらわされる。この直線が楕円曲線と交わるもう一つの点をR=(x3,y3)とすると、P+Q=-R=(x3,-y3) である。最初にx3を求める。

より、x3の次数に沿って整理すると、

ここで、b’、c'はx1,x2,y1,y2の有理式。根と係数の関係より、

また、y3については

である。したがって、

本当は、x3などは使わずもっと直接的に書きたかったが、見通しが悪くなるのでやめた。
○ x1=x2 の場合
P≠Qであれば、P+Qは原点。
P=Qのときは、Pで楕円曲線に対する接線を引き、楕円曲線と接線とのもう一つの交点をR=(x3,y3)とすると、P+Q=-Rである。楕円曲線の方程式を微分して

よって、接線の方程式は、

楕円曲線と接線の交点は、

より、

ここで、b‘’、c‘’はx1,y1の有理式。根と係数の関係より、

また、y3については

よって、

である。最初に大見えを切った割には大した結果になりませんでした。悪しからず。









