どもども。
前回に続いて今年の東北大入試理系数学第1問をやっていきます
問題はこちら

前回:http://blog.goo.ne.jp/mathnegi/e/33187e612de08726a749204fe231aac2
s,tという2つのパラメータに依存してx,yが動くという状況でした~
(2)を今回はやりますよ~
基本的には前回と同じ手法が使える(考え方4は使えないっすね )ので,前回と同じ解法の順序でやっていってみましょう~
)ので,前回と同じ解法の順序でやっていってみましょう~
 考え方1
考え方1
(X,Y)という点が答えの領域に含まれているならば X=st+s-t+1,Y=s+t-1 を満たす
何かしらの実数s,tが存在するはずだ,それを具体的に求めてしまうことでそのようなs,tの存在性を実証しよう,
こういう発想でやってみます
s,tについて解いてしまえばいいんですが2次方程式が出てくるので,
その解は√を含んだ式になってしまいます。
根号内が非負でありさえすれば,その解は実数になるので
判別式≧0をすればよいわけですね


 考え方2
考え方2
2つもあるパラメータが邪魔なので一旦1つにしてしまう方針です
x=st+s-t+1…… ,y=s+t-1……
,y=s+t-1……
からsを消去すると
x=(y-t+1)t+(y-t+1)-t+1……
が出てきます。tを消去すると
x=s(y-s+1)+s-(y-s+1)+1……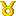
が出てきます。
「 かつ
かつ 」を考える代わりに
」を考える代わりに
「 かつ
かつ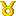 」 を考えるのですが
」 を考えるのですが
ちょっと面倒そうなので,更に代わりに
「 かつ
かつ 」を考えることにします
」を考えることにします
 から,y={1/(t+1)}x-{2/(t+1)}+tが得られますが,
から,y={1/(t+1)}x-{2/(t+1)}+tが得られますが,
分母が0になるt=-1の場合は別に考えなきゃいけません。
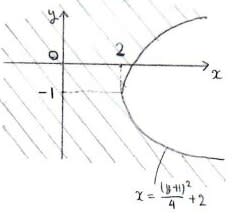
まずはt≠-1の場合について考えます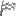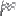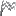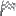
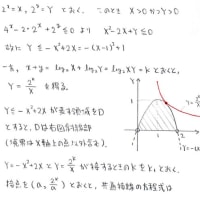
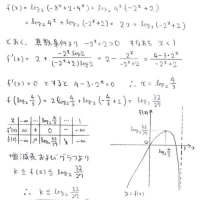
tがあれこれ動いたときに,直線x=x_0上でyがどのような範囲を動くのか考察します。


x_0と2の大小によって状況が変わるようですね


x_0=2のときは,そもそもf(t)=tになってしまいます

次はt=-1の場合を考えます。このときは直線x=2を表すみたいです

あとはまとめればOKですね
ただし についても触れなくてはいけません。
についても触れなくてはいけません。
tが実数全体を動いたときに を満たす(x,y)の存在域は上の考察から分かりますが
を満たす(x,y)の存在域は上の考察から分かりますが
その領域上の各点(X,Y)とtに対してsを によって定めることが出来るので
によって定めることが出来るので
「 かつ
かつ 」を満たす(x,y)の存在域もまた上で求めた領域と一致してしまいます
」を満たす(x,y)の存在域もまた上で求めた領域と一致してしまいます


ちなみに,「 かつ
かつ 」を考えると,
」を考えると,
どちらも同じ領域が出てきます
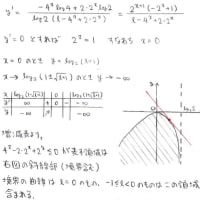
xをx=x_0に固定するのではなく,yをy=y_0に固定してもOKです,
というかそっちのほうが2次関数なので簡単です
その場合の計算はほぼ次に挙げる解法と変わらなくなります~
 考え方3
考え方3
すべての実数を動くs,tを変数とする2変数関数y(s,t)=s+t-1の値域は全実数です。
そこでYを定数として,y(s,t)=Yを満たすs,tに限定してx(s,t)=st+s-t+1の値域を考える方針です
s=-t+Y+1であるので,x(-t+Y+1,t)の値域を考えればよいわけですね

 考え方4
考え方4
2次方程式が実数解を持つ条件の議論を利用した解法です。
まぁ,考え方1と大体同じですが~
s-1とt+1の和と積が与えられているとみなします

あとは図を描くだけですね
前回に続いて今年の東北大入試理系数学第1問をやっていきます

問題はこちら


前回:http://blog.goo.ne.jp/mathnegi/e/33187e612de08726a749204fe231aac2
s,tという2つのパラメータに依存してx,yが動くという状況でした~
(2)を今回はやりますよ~

基本的には前回と同じ手法が使える(考え方4は使えないっすね
 )ので,前回と同じ解法の順序でやっていってみましょう~
)ので,前回と同じ解法の順序でやっていってみましょう~ 考え方1
考え方1(X,Y)という点が答えの領域に含まれているならば X=st+s-t+1,Y=s+t-1 を満たす
何かしらの実数s,tが存在するはずだ,それを具体的に求めてしまうことでそのようなs,tの存在性を実証しよう,
こういう発想でやってみます

s,tについて解いてしまえばいいんですが2次方程式が出てくるので,
その解は√を含んだ式になってしまいます。
根号内が非負でありさえすれば,その解は実数になるので
判別式≧0をすればよいわけですね



 考え方2
考え方22つもあるパラメータが邪魔なので一旦1つにしてしまう方針です

x=st+s-t+1……
 ,y=s+t-1……
,y=s+t-1……
からsを消去すると
x=(y-t+1)t+(y-t+1)-t+1……

が出てきます。tを消去すると
x=s(y-s+1)+s-(y-s+1)+1……
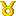
が出てきます。
「
 かつ
かつ 」を考える代わりに
」を考える代わりに「
 かつ
かつ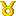 」 を考えるのですが
」 を考えるのですがちょっと面倒そうなので,更に代わりに
「
 かつ
かつ 」を考えることにします
」を考えることにします
 から,y={1/(t+1)}x-{2/(t+1)}+tが得られますが,
から,y={1/(t+1)}x-{2/(t+1)}+tが得られますが,分母が0になるt=-1の場合は別に考えなきゃいけません。
まずはt≠-1の場合について考えます
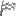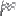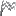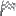
tがあれこれ動いたときに,直線x=x_0上でyがどのような範囲を動くのか考察します。


x_0と2の大小によって状況が変わるようですね



x_0=2のときは,そもそもf(t)=tになってしまいます


次はt=-1の場合を考えます。このときは直線x=2を表すみたいです


あとはまとめればOKですね

ただし
 についても触れなくてはいけません。
についても触れなくてはいけません。tが実数全体を動いたときに
 を満たす(x,y)の存在域は上の考察から分かりますが
を満たす(x,y)の存在域は上の考察から分かりますがその領域上の各点(X,Y)とtに対してsを
 によって定めることが出来るので
によって定めることが出来るので「
 かつ
かつ 」を満たす(x,y)の存在域もまた上で求めた領域と一致してしまいます
」を満たす(x,y)の存在域もまた上で求めた領域と一致してしまいます



ちなみに,「
 かつ
かつ 」を考えると,
」を考えると,どちらも同じ領域が出てきます

xをx=x_0に固定するのではなく,yをy=y_0に固定してもOKです,
というかそっちのほうが2次関数なので簡単です

その場合の計算はほぼ次に挙げる解法と変わらなくなります~

 考え方3
考え方3すべての実数を動くs,tを変数とする2変数関数y(s,t)=s+t-1の値域は全実数です。
そこでYを定数として,y(s,t)=Yを満たすs,tに限定してx(s,t)=st+s-t+1の値域を考える方針です

s=-t+Y+1であるので,x(-t+Y+1,t)の値域を考えればよいわけですね


 考え方4
考え方42次方程式が実数解を持つ条件の議論を利用した解法です。
まぁ,考え方1と大体同じですが~

s-1とt+1の和と積が与えられているとみなします

あとは図を描くだけですね













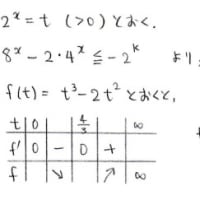


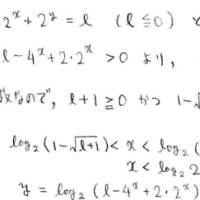

※コメント投稿者のブログIDはブログ作成者のみに通知されます