６の５０乗の最高位の数字は
いくつになるでしょうか？
電卓を使えば簡単に求められますが，
数学的に常用対数２や３を使って
求める方法があったら教えて下さい。
私も考え中です。
いくつになるでしょうか？
電卓を使えば簡単に求められますが，
数学的に常用対数２や３を使って
求める方法があったら教えて下さい。
私も考え中です。
最新の画像［もっと見る］
-
明けましておめでとうございます
5年前
-
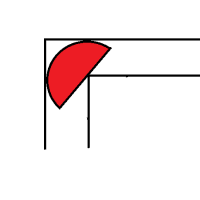私から、夏休みの宿題
12年前
-
この面積を求めよ
16年前
-
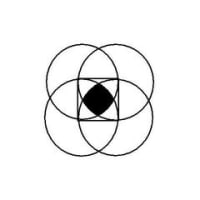
ボイドキューブ
16年前
-
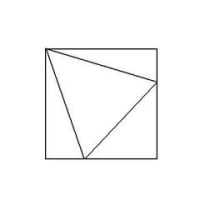正方形に内接する正三角形は？
17年前
-
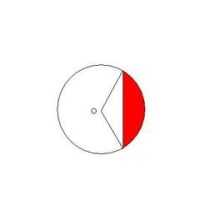円の面積を３等分せよ
18年前
-
宮城県白石城
19年前
-
１０円まんじゅう
19年前
-
楽天
19年前
-
蘭を買いました
19年前
a=10^log(10)a…①より，
6^50
=｛10^log(10)6｝^50
=10^50log(10)6…(*)
ここで，
log(10)6
=log(10)2+log(10)3
=0.778より(*)は，
10^38.908=10^0.908×10^38
また，
log(10)8=2log(10)2=0.903
log(10)9=2log(10)3=0.954より，
log(10)8<0.908<log(10)9
10^log(10)8<10^0.908<10^log(10)9
①より，
8<10^0.908<9
つまり10^0.908の最高位は8であるから，
6^50=(0.8…)×10^38
従って答えは8である。（終）
ちなみに①は両辺の常用対数を取ればすぐ証明出来ますよ。
※URLがないのでこのページのを使ってしまいました。ゴメンなさい・・・・
log(10)8<0.908<log(10)9
10^log(10)8<10^0.908<10^log(10)9
①より，
8<10^0.908<9
つまり10^0.908の最高位は8であるから，
6^50=(0.8…)×10^38
従って答えは8である。（終）
ちなみに①は両辺の常用対数を取ればすぐ証明出来ますよ。
※URLがないのでこのページのを使ってしまいました。ゴメンなさい。
10^log(10)8<10^0.908<10^log(10)9
①より，
8<10^0.908<9
つまり10^0.908の最高位は8であるから，
6^50=(0.8…)×10^38
従って答えは8である。（終）
ちなみに①は両辺の常用対数を取ればすぐ証明出来ますよ。
※URLがないのでこのページのを使ってしまいました。ゴメンなさい。
10^log(10)8<10^0.908<10^log(10)9
①より，
8<10^0.908<9
つまり10^0.908の最高位は8であるから，
6^50=(0.8…)×10^38
従って答えは8である。（終）
ちなみに①は両辺の常用対数を取ればすぐ証明出来ますよ。
※URLがないのでこのページのを使ってしまいました。ゴメンなさい。
10^log(10)8<10^0.908<10^log(10)9
①より，
8<10^0.908<9
つまり10^0.908の最高位は8であるから，
6^50=(0.8…)×10^38
従って答えは8である。（終）
ちなみに①は両辺の常用対数を取ればすぐ証明出来ますよ。
※URLがないのでこのページのを使ってしまいました。ゴメンなさい。
8<10^0.908<9
よって
6^50=(0.8…)×10^38
従って答えは８です。
log(10)9=2log(10)3=0.954より，
log(10)8<0.908<log(10)9
10^log(10)8<10^0.908<10^log(10)9
①より，
8<10^0.908<9
つまり10^0.908の最高位は8であるから，
6^50=(0.8…)×10^38
従って答えは8である。（終）
ちなみに①は両辺の常用対数を取ればすぐ証明出来ますよ。
※何回も無駄なコメントを出してしまって本当にゴメンなさい…。
最高位はどうも８のようです