■ごめんなさい。今日は、ちょっとマニアックなネタです。

①式はアレニウスの式と言われている式。ある絶対温度Tにおける化学反応の速さを表してる。簡単に言うと、多くの化学反応は、温度が上がると指数関数的に、その速度は速くなるよ。と言うことを表している。また、この式は、化学反応だけでなく、色々な物が劣化する速さにも当てはまるらしい。これを用いて、色々な物(工業製品等)の耐久試験において、温度を上げることにより試験時間を短縮させる根拠として用いられている。
①式は速度定数を表すが、その逆数(劣化速度の逆数)をとると、それは、その物の寿命(信頼性を維持できる時間)を表現していると言える。②式のようになる。(逆数にするのだから、指数部の符号を反対にすればよい。)
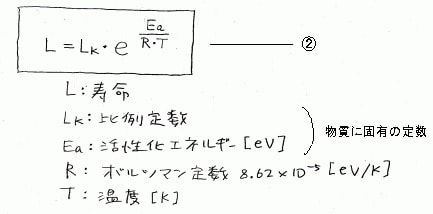
■さらに、胡散臭い寿命定数Lkを消去するために、温度の異なる2つの物(温度Tmと温度Tnの物)の寿命の比で考えることにする。温度Tmである物Mの寿命Lmと 、温度Tnである物Nの寿命Lnとの比は下の③式のようになる。
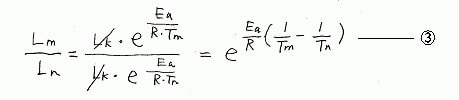
■ところで、僕たち、人間の生命活動も、無数の化学反応の結集と考えることができる。で、ふと、体温の違いにより寿命がどれだけ変わってくるのかをアレニウスの式で推定できないものか?と思いついた。で、③式を用いて計算してみる。
ここで問題になるのは、生物(人間)の生命活動での活性化エネルギーはどれくらいの値?という疑問。ネットで検索すれども、明確な値などない。そもそも、アレニウスの式における活性化エネルギーというもの自体がやや不明確な存在。でも、とある信頼性試験関連の文献に「腐食、腐敗劣化における活性化エネルギーは0.3~0.4eV」とあった。これは、なんとなく生物活動に近い雰囲気なので、とりあえず、この値で計算してみることにする。
例えば、体温35.5℃のMさんと、体温37℃のNさんとの寿命を比較してみよう!
Tm=35.5+273=308.5K、Tn=37+273=310K、Ea=0.4eV、R=8.62*10^(-5)eV/Kを③式に代入すると
Lm/Ln=1.075 となる。
つまり、体温35.5℃のMさんは、体温37℃のNさん よりも約8%長生きできるということ。体温37℃のNさんが80歳まで生きたなら、体温35.5℃のMさんは86歳まで生きれる。つまり1.5℃体温が低いと、6年寿命が長くなるという結果になる。
みんな体温を下げて長生きしよう!!
C.F.
これは、なぜか寝付けぬ雨の夜に、適当-に考えただけなので、適当-に読んでね。
C.F.その2
ネットで検索したが、アレニウスの式を人間に寿命に適応した記事や論文は、未だないようだ。なぜだろう?生物は、そんな単純なものでは無いのだろうか??でも、化学反応系の集合体としてとらえても、あながち間違いでもないような気もするなあ。
ご挨拶とメニュー

①式はアレニウスの式と言われている式。ある絶対温度Tにおける化学反応の速さを表してる。簡単に言うと、多くの化学反応は、温度が上がると指数関数的に、その速度は速くなるよ。と言うことを表している。また、この式は、化学反応だけでなく、色々な物が劣化する速さにも当てはまるらしい。これを用いて、色々な物(工業製品等)の耐久試験において、温度を上げることにより試験時間を短縮させる根拠として用いられている。
①式は速度定数を表すが、その逆数(劣化速度の逆数)をとると、それは、その物の寿命(信頼性を維持できる時間)を表現していると言える。②式のようになる。(逆数にするのだから、指数部の符号を反対にすればよい。)

■さらに、胡散臭い寿命定数Lkを消去するために、温度の異なる2つの物(温度Tmと温度Tnの物)の寿命の比で考えることにする。温度Tmである物Mの寿命Lmと 、温度Tnである物Nの寿命Lnとの比は下の③式のようになる。
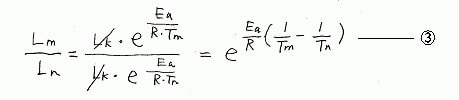
■ところで、僕たち、人間の生命活動も、無数の化学反応の結集と考えることができる。で、ふと、体温の違いにより寿命がどれだけ変わってくるのかをアレニウスの式で推定できないものか?と思いついた。で、③式を用いて計算してみる。
ここで問題になるのは、生物(人間)の生命活動での活性化エネルギーはどれくらいの値?という疑問。ネットで検索すれども、明確な値などない。そもそも、アレニウスの式における活性化エネルギーというもの自体がやや不明確な存在。でも、とある信頼性試験関連の文献に「腐食、腐敗劣化における活性化エネルギーは0.3~0.4eV」とあった。これは、なんとなく生物活動に近い雰囲気なので、とりあえず、この値で計算してみることにする。
例えば、体温35.5℃のMさんと、体温37℃のNさんとの寿命を比較してみよう!
Tm=35.5+273=308.5K、Tn=37+273=310K、Ea=0.4eV、R=8.62*10^(-5)eV/Kを③式に代入すると
Lm/Ln=1.075 となる。
つまり、体温35.5℃のMさんは、体温37℃のNさん よりも約8%長生きできるということ。体温37℃のNさんが80歳まで生きたなら、体温35.5℃のMさんは86歳まで生きれる。つまり1.5℃体温が低いと、6年寿命が長くなるという結果になる。
みんな体温を下げて長生きしよう!!
C.F.
これは、なぜか寝付けぬ雨の夜に、適当-に考えただけなので、適当-に読んでね。
C.F.その2
ネットで検索したが、アレニウスの式を人間に寿命に適応した記事や論文は、未だないようだ。なぜだろう?生物は、そんな単純なものでは無いのだろうか??でも、化学反応系の集合体としてとらえても、あながち間違いでもないような気もするなあ。
ご挨拶とメニュー



















