久しぶりにパズル本を作りました。今度はナンプレではなく、「足し算クロス」(カックロ、サムクロスとも呼ばれる)という、ナンプレと同じころに日本に入ってきたパズルです。
パズルの詳しい説明はこちらをごらんください。
「足し算クロス」の説明
問題のサンプルはこちら。「ぱずぷれ」へのリンクです。
やさしい
ふつう
ちょっとむずかしい
ハガキサイズ43問入り150円。「発明家ショップトキメキ」で買えます。
私から直接買う場合は100円です。常に持ち歩くので、興味がある方は声をかけてください。
単一組み合わせ(組み合わせが1通りの連続マス)の一覧です。
| 長さ | 和 | 数字 |
| 2 | 3 | 1 2 |
| 4 | 1 3 | |
| 16 | 7 9 | |
| 17 | 8 9 | |
| 3 | 6 | 1 2 3 |
| 7 | 1 2 4 | |
| 23 | 6 8 9 | |
| 24 | 7 8 9 | |
| 4 | 10 | 1 2 3 4 |
| 11 | 1 2 3 5 | |
| 29 | 5 7 8 9 | |
| 30 | 6 7 8 9 | |
| 5 | 15 | 1 2 3 4 5 |
| 16 | 1 2 3 4 6 | |
| 34 | 4 6 7 8 9 | |
| 35 | 5 6 7 8 9 | |
| 6 | 21 | 1 2 3 4 5 6 |
| 22 | 1 2 3 4 5 7 | |
| 38 | 3 5 6 7 8 9 | |
| 39 | 4 5 6 7 8 9 | |
| 7 | 28 | 1 2 3 4 5 6 7 |
| 29 | 1 2 3 4 5 6 8 | |
| 41 | 2 4 5 6 7 8 9 | |
| 42 | 3 4 5 6 7 8 9 | |
| 8 | 36 | 1 2 3 4 5 6 7 8 |
| 37 | 1 2 3 4 5 6 7 9 | |
| 38 | 1 2 3 4 5 6 8 9 | |
| 39 | 1 2 3 4 5 7 8 9 | |
| 40 | 1 2 3 4 6 7 8 9 | |
| 41 | 1 2 3 5 6 7 8 9 | |
| 42 | 1 2 4 5 6 7 8 9 | |
| 43 | 1 3 4 5 6 7 8 9 | |
| 44 | 2 3 4 5 6 7 8 9 | |
| 9 | 45 | 1 2 3 4 5 6 7 8 9 |
足し算クロスの説明トップへ
二択のペア
ひとつの連続マスに同じ数字からなる二択のマスが2個ある場合、他のマスにはその二つの数は入りません。
★印のマスには、どちらかが7でどちらかが9になります。どちらになっても、A,B,C,Dには7と9は入りません。和が24で長さ3の連続マスの組み合わせは7,8,9の1通りなので、Dには8が入ります。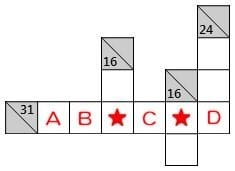
★印のマスには、どちらかが7でどちらかが9になります。どちらになっても、A,B,Cの合計は23-(7+9)=7になります。したがってA,B,Cに入る数の組み合わせは1,2,4の1通りです。Bには2と4は入らないので、1に決まります。
三択のトリオ
ひとつの連続マスに同じ数字3個からなる三択のマスが3個ある場合、他のマスにはその三つの数は入りません。3個の数字のうちすべてではなく、その中の2個のどちらかが入る場合もあります。
Aに入る数は1か2、Cに入る数字は1か3、Eに入る数字は1か2か3です。A、C、Eに入る数字がどれになってもBとDには1,2,3は入りません。したがってBとDの和は22-(1+2+3)=16になり、BとDは一方が7で他方が9になります。
二択の連鎖
二択のマスによって同じ連続マスの他のマスも二択になり、それが連鎖し、連鎖の先のほうで数が決まり、最初の二択が決定することがあります。
Aに入る数は3か4です。Aが3ならBは6、Aが4ならBは5になります。Bには6は入らないので、Aは3ではなく、4になります。
Aには3か5が入ります。Aが3のとき、Bは6、Cは1、Dは9、Eは2になります。Aが5のとき、Bは4、Cは3、Dは7、Eは4になります。Eに4が入ると和が13の連続マスに4が2個になってしまうので、Eに4は入りません。連鎖をさかのぼって、Aは3に決まります。
二択と和の保存
ある連続マスに二択のマスがあって、そのどちらを選んでも別の連続マスの二つのマスの和が同じになる場合があります。
AとBは一方が1で他方が3です。AとDには2が入らないので、Fは2に決まります。A=3のとき、B=1、D=1、E=7となります。A=1のとき、B=3、D=3、E=5となります。いずれにしてもD+E=8となります。したがってC=15-2-8=5となり、Eに5は入らず7になり、B=1、A=3、D=1となります。
井桁
4つの連続マスが井桁状に組み合わさっていて、その中の上下あるいは左右の2つの連続マスで、同じ数字Xが交点のどちらかに入る場合、直行する2つの連続マスは交点以外のマスにXは入りません。ナンプレのX-wing(別名井桁、対角線)と同じようなテクニックです。
AとBのどちらかに1が入ります。CとDのどちらかにも1が入ります。もし★のマスのどれかに1が入ると、AとCには1が入れられないのでBとDの両方に1を入れなければならず、矛盾が生じます。したがって★に1は入りません。同様に◇にも1は入りません。よってEには1が入ります。
和が29の連続マスの左側の2マスには9が入らないので、AとBのどちらかに9が入ります。CとDのどちらかにも9が入ります。前の例と同様に★と◇には9は入りません。Eは9になります。
足し算クロスの説明トップへ
足し算クロスの説明トップへ
部分連続マスの単一組み合わせ
連続マスの一部が決まっているとき、残りのマスの合計によって入る数字の組み合わせが1通りになることがあります。
[例]
A,B,Cの合計は22-8-7=7です。したがって、A,B,Cに入る数字の組み合わせは1,2,4に決まり、Bに入る数字は1に決まります。
複数マスの上限・下限
連続マスの長さによって合計の最大値・最小値が決まります。
[例]
3マスの合計の最小値は1+2+3=6です。和が12で長さ4の連続マスにもし7以上の数を入れると、残りの3マスの合計が5以下になってしまいます。したがってAには6以下の数しか入れられません。和が23で長さが3の連続マスの組み合わせは6,8,9の1通りなので、Aは6に決まります。
3マスの合計の最大値は7+8+9=24です。和が27で長さ4の連続マスにもし2以下の数を入れると、残りの3マスの合計が25以上になってしまいます。したがってAには2以下の数しか入れられません。和が6で長さが3の連続マスの組み合わせは1,2,3の1通りなので、Aは3に決まります。
足し算クロスの説明トップへ
足し算クロスの説明トップへ
赤い数字はそのテクニックで決まる数字です。
単一組み合わせの単一交差
それぞれ組み合わせが1通りしかない2つの和で、共通する数字が1個しかない場合、それらが交差するマスはその共通する数字になります。
[例]
長さ2で和が3の連続マスの組み合わせは 1,2 の1通り、長さ2で和が4の連続マスの組み合わせは 1,3 の1通りなので、それらの交点は1になります。
同様のテクニックでよく使われるものを挙げておきます。
単一組み合わせ一覧
1マスの上限・下限
あるマスに数字Xを入れることによって、そのマスを含む連続マスのどれかが0以下になったり10以上になってしまう場合、そのマスにXは入れられません。
[例]
Aに8と9を入れることはできません。Bが0以下になってしまうからです。
Aに1と2を入れることはできません。Bが10以上になってしまうからです。
単一組み合わせの単一マス
組み合わせが1通りしかない連続マスで、ある数字を入れることができるマスが1個しかない場合、そのマスはその数字になります。
[例]
和が15になる長さ5の連続マスは、組み合わせが 1,2,3,4,5 の1通りです。×印のマスには5を入れることができないので、左から4番目のマスは5に決まります。
和が30になる長さ4の連続マスは、組み合わせが 6,7,8,9 の1通りです。×印のマスには8を入れることができないので、上から3番目のマスは8に決まります。
単一組み合わせの単一数字
組み合わせが1通りしかない連続マスで、ひとつの数字以外が入らない場合です。
[例]
和が16で長さ5の連続マスは組み合わせが1,2,3,4,6の1通りです。Aには1,2,3,4が入らないので、6に決まります。
最後の1マス
連続マスの1マス以外が決まっているとき、最後の1マスは全体の和から決まっているマスの和を引いた数になります。
[例]
15-(1+5+6)=3 なので、Aには3が入ります。
数の重複の回避
ある数を入れることによって決まる他のマスの数が連続マスの中で重複する場合、その数は入れられません。
[例]
Aに6を入れるとBも6になってしまうので、Aには6は入りません。
Aに3を入れるとBが4になってしまうので、Aに3は入りません。
足し算クロスの説明トップへ
赤い数字はそのテクニックで決まる数字です。
単一組み合わせの単一交差
それぞれ組み合わせが1通りしかない2つの和で、共通する数字が1個しかない場合、それらが交差するマスはその共通する数字になります。
[例]
長さ2で和が3の連続マスの組み合わせは 1,2 の1通り、長さ2で和が4の連続マスの組み合わせは 1,3 の1通りなので、それらの交点は1になります。
同様のテクニックでよく使われるものを挙げておきます。
単一組み合わせ一覧
1マスの上限・下限
あるマスに数字Xを入れることによって、そのマスを含む連続マスのどれかが0以下になったり10以上になってしまう場合、そのマスにXは入れられません。
[例]
Aに8と9を入れることはできません。Bが0以下になってしまうからです。
Aに1と2を入れることはできません。Bが10以上になってしまうからです。
単一組み合わせの単一マス
組み合わせが1通りしかない連続マスで、ある数字を入れることができるマスが1個しかない場合、そのマスはその数字になります。
[例]
和が15になる長さ5の連続マスは、組み合わせが 1,2,3,4,5 の1通りです。×印のマスには5を入れることができないので、左から4番目のマスは5に決まります。
和が30になる長さ4の連続マスは、組み合わせが 6,7,8,9 の1通りです。×印のマスには8を入れることができないので、上から3番目のマスは8に決まります。
単一組み合わせの単一数字
組み合わせが1通りしかない連続マスで、ひとつの数字以外が入らない場合です。
[例]
和が16で長さ5の連続マスは組み合わせが1,2,3,4,6の1通りです。Aには1,2,3,4が入らないので、6に決まります。
最後の1マス
連続マスの1マス以外が決まっているとき、最後の1マスは全体の和から決まっているマスの和を引いた数になります。
[例]
15-(1+5+6)=3 なので、Aには3が入ります。
数の重複の回避
ある数を入れることによって決まる他のマスの数が連続マスの中で重複する場合、その数は入れられません。
[例]
Aに6を入れるとBも6になってしまうので、Aには6は入りません。
Aに3を入れるとBが4になってしまうので、Aに3は入りません。
足し算クロスの説明トップへ
