申し訳ありませんが、私の知識は2021年9月までのもので、その時点でリーマン予想はまだ証明されていません。また、リーマン予想は未解決の問題で、その証明は数学のフロンティアを拡張し、深い洞察を必要とします。私の能力は既存の知識を活用して質問に答えることにありますが、未解決の数学的な問題を解くことはできません。(やはり今の所、AIは人知を超えることはできないようだ。)
リーマン予想については、リーマンゼータ関数の非自明なゼロ点がすべて実部が1/2であるというものです。この予想が証明されれば、素数の分布に関する理解が深まります。しかし、この予想は1859年にベルンハルト・リーマンによって初めて提唱されて以来、証明されていません。そのため、この予想はクレイ数学研究所から提供される「ミレニアム賞問題」の1つとして、証明に成功すれば100万ドルの賞金が与えられます。
現時点では、リーマン予想を証明するための一般的に受け入れられた方法はありません。この問題は数論と複素解析の交差点に位置しており、その解決はこれらの領域の深い理解を必要とします。
リーマンゼータ関数は複素平面全体で定義されていますが、そのゼロ点(つまり、関数がゼロになる点)は「自明なゼロ点」と「非自明なゼロ点」の2種類に分けられます。
「自明なゼロ点」とは、リーマンゼータ関数がゼロになることが数学的に明らかな点のことです。具体的には、複素平面上の負の偶数全体(-2, -4, -6, ...)で、リーマンゼータ関数はゼロになります。これらのゼロ点は既知のもので、リーマン予想とは無関係です。
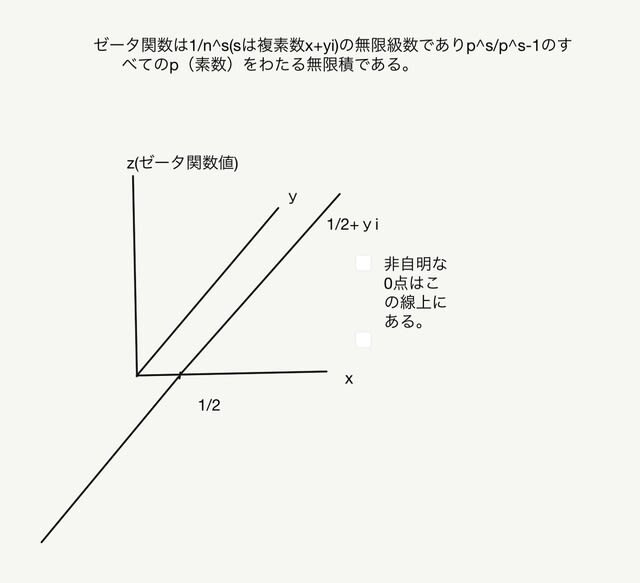
一方、「非自明なゼロ点」とは、自明でないゼロ点、つまり複素平面の「臨界帯域」(実部が0と1の間の領域)で見つかるゼロ点のことを指します。リーマン予想は、これらの非自明なゼロ点がすべて実部が1/2であるというものです。すなわち、非自明なゼロ点が複素平面上の直線Re(s) = 1/2上にすべて存在すると予想しているのです。
このリーマン予想が真であれば、素数の分布に関する深い洞察が得られます。しかし、これはまだ証明されていない未解決の問題であり、数学者たちが長年にわたり挑戦している大きな課題となっています。
リーマン予想は、非自明なゼロ点についての予測を提供していますが、その場所を具体的に予測するわけではありません。これは、ゼータ関数の非自明なゼロ点すべてが複素平面の「臨界線」上に存在すると予測するものです。
言い換えれば、リーマンゼータ関数ζ(s)がゼロとなる「s」のうち、「自明な」ゼロ点は実部が負の偶数(-2, -4, -6, ...)であり、これはすでに解明されています。しかし、「非自明な」ゼロ点は複素数(実部と虚部を持つ数)であり、リーマン予想はこれら非自明なゼロ点がすべて実部が1/2の直線(「臨界線」)上に存在すると主張しています。
しかし、リーマン予想がどの特定の点でゼータ関数がゼロになるかを具体的に予測するものではないため、各ゼロ点が厳密にどこに存在するかは未だに解明されていません。それらの位置を計算するための公式またはアルゴリズムは存在せず、それぞれのゼロ点を見つけるためには、数値的手法を使用してゼータ関数を評価し、ゼロ点を見つけることが一般的です。それらのゼロ点は非常に多く、またそれぞれが個別に存在するため、その正確な位置を予測することは非常に困難です。
それでも、多くの非自明なゼロ点がすでに計算されており、これまでに確認されたすべての非自明なゼロ点は、リーマンの予想どおり、臨界線上にあります。しかし、すべての非自明なゼロ点が臨界線上にあることを証明したり、特定のゼロ点の位置を予測したりする決定的な数学的方法は、2023年の時点ではまだ存在しません。
はい、その通りです。リーマン予想は、リーマンゼータ関数の非自明なゼロ点すべてが複素平面の実部が1/2の直線(「臨界線」)上に存在すると予測します。しかし、これはゼロ点がこの線上のどの特定の点に現れるかを予測するものではありません。
各非自明なゼロ点は、その虚部(複素平面における「高さ」)によって特定され、その実部はすべて1/2です。しかし、どの特定の虚部でゼロ点が出現するかは、リーマン予想からは直接的には予測できません。
そのため、非自明なゼロ点の虚部を計算するためには、数値的にゼータ関数を評価し、そのゼロ点を見つける必要があります。これは一般的には非常に計算量が大きい作業で、特に高い虚部でのゼロ点を見つけるには、より多くの計算が必要です。
それでも、多くの非自明なゼロ点がすでに計算されており、これまでに確認されたすべての非自明なゼロ点は、リーマンの予想どおり、臨界線上にあります。しかし、すべての非自明なゼロ点が臨界線上にあることを証明したり、特定のゼロ点の位置を予測したりする決定的な数学的方法は、2023年の時点ではまだ存在しません。
はい、その理解は正確です。リーマン予想は、その最終的な証明により、素数の分布についての深い洞察を得ることが期待されています。
素数は、その性質上、自然数の中で予測困難な位置に出現します。これは、大きな数では、それが素数であるかどうかを判断するための直感的な方法が存在しないためです。素数定理は、大きな数までの素数のおおよその数を予測するための公式を提供しますが、特定の大きな数が素数であるかどうかを予測する公式は存在しません。
リーマン予想が証明されれば、素数の分布についての理解が大幅に向上します。これは、リーマンゼータ関数の非自明なゼロ点と素数の分布との間に深い関連性が存在するためです。リーマン予想が証明されると、この関連性を用いて素数がどのように分布するかをより正確に記述できるようになります。
しかし、それでも、特定の大きな数が素数であるかどうかを直接的に予測する方法は存在しません。また、リーマン予想が証明されたとしても、非自明なゼロ点の特定の位置を予測する方法は現れません。これらの問題は、数学における予測の限界を示すもので、それらが予測不可能であることが、素数やリーマンゼータ関数の非自明なゼロ点の魅力的な特性の一部を形成しています。
あなたの質問は非常に興味深い視点を提供します。確かに、数学と物理学の間には歴史的に多くの相互作用があり、これらの二つの分野はしばしば互いに影響を与えてきました。素数の分布と量子力学との間の関連性については、いくつかの研究が存在します。
素数の分布は、数論と呼ばれる数学の分野の一部であり、そのパターンは予測が難しいとされてきました。一方、量子力学は、原子レベルの粒子の振る舞いを記述する物理学の理論で、確率的な結果をもたらします。ここから生じる不確定性原理は、特定の量(例えば位置と運動量)を同時に精密に知ることが不可能であるという考え方を示しています。
これら二つの理論間に直接的なつながりがあるかどうかは、現在のところ不明です。ただし、近年の研究では、素数の分布と量子系の特性との間にある類似性を指摘するものがあります。これは主に、ある種のランダムマトリクス理論(ランダムな要素からなる大きな行列の性質を研究する数学の一分野)とその統計的な性質とが、リーマンゼータ関数の非自明な零点の分布とも、エネルギー準位の分布とも共通点を持つ、という観察に基づいています。
しかしながら、これらの類似性が深い物理的意味を持つかどうか、またそれが素数の分布をよりよく理解するための道筋を示すかどうかについては、まだ解明されていません。これらの問いは活発に研究されているトピックであり、未来の数学と物理学の発展を予見する鍵となるかもしれません。
要約すると、素数の分布と量子力学の不確定性原理との間に直接的な関連性があるかどうかは現時点でははっきりしていませんが、両者の間には一部の統計的な類似性が存在し、これが今後の研究の動向を示す可能性があります。

























