食塩水の問題２ 面積図で解く①

食塩水の濃度は
食塩水全体の量×濃度＝溶けている食塩の量
というかけ算の式ができますので、面積図で解く事ができます。
イメージはこんな感じです。

イメージですので、縦×横をしても本当の食塩の量は計算できません‥

面積図で解く問題は「食塩水」に何かを足す、または引く問題のときです。
「水」に食塩を足す、という問題は前回紹介した計算で解きましょう。

「食塩水」に何かを足す、または引く問題には次の４種類があります。
①食塩水＋水
②食塩水－水
③食塩水＋食塩
④食塩水＋食塩水

今回は①の「食塩水＋水」を見てみましょう。

問：１２％の食塩水２００gに水を１００g加えました。何％になりますか。

まず「１２％の食塩水２００g」をかきます。


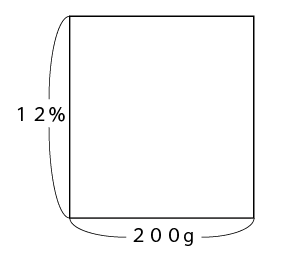
次に加えた水１００gをかき加えます。

水の濃度は０％ですので、横線だけになります。

新しく長方形をつくります。

この横長の長方形は、食塩水に水を足してできあがった新しい食塩水です。
元々の長方形の面積は「溶けている食塩の量」を表していました。
水を加えても溶けている食塩の量は変わらないので、
この横長の長方形の面積は、元の長方形と同じ面積になります。

濃度をかき加えます。


これで面積図は出来上がりです。
２つの長方形の面積が同じことを利用して解いていきます。
縦長の長方形の面積は
１２×２００＝２４００
横長の長方形の横の長さは
２００＋１００＝３００
よって□は
□×３００＝２４００
　　　 □＝８　　　　　　　８％　

面積図を使うと、小数の計算をしなくてもすむので、ちょっと楽です。

ちなみにこの問題を式だけで解くと
２００×０.１２＝２４
２００＋１００＝３００
２４÷３００＝０.０８（３００×□＝２４）　 　　８％　
となります。

次回は　②食塩水－水　です。