単振子の運動 (0)

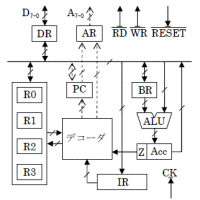
phys.pdf phys-s.pdf 記事一覧

折れ線近似

sys.pdf は離散系を対象としているため，微分方程式の離散近似について phys-s.pdf で補足することを予定しています．このため，しばらく sys.pdf から離れます．ただし，内容についてはウソを書く可能性が高いので．自分の頭でしっかり考えてください．

タイトルに示したように，例として researchmap のブログ[1]でとりあげた単振子を考えます．簡単のために m g = 1 である質点が振動の角周波数が 1 となる長さの糸で吊るされているとして一般化座標θで表した運動方程式が

   θ'(t) = ω(t),    ω'(t) = －sin θ(t)

で表されるとします．力学的エネルギー

   E(t) = (1/2){ω(t)}² + {1 － cos θ(t)}

が保存されること，すなわち E'(t) = 0 が成立することは容易に確かめられます．厳密解は第１種楕円積分を用いて表現できますが，厳密解は未知扱いにします．

[1] 保存系の離散近似
  http://researchmap.jp/jooj2baak-529/#_529
[2] 広田良吾，高橋大輔，差分と超離散，ISBN4-320-01729-3，第３章前半．
  http://www.kyoritsu-pub.co.jp/shinkan/shin0302_06.html
  主としてこれを参照します．Web 上の資料でなくてすみません．
[3] II. 非線形振動
  http://web.mac.com/takeda_t/Bonryu/Lecture_files/TCSE4~5.pdf

難しい話はできません．次のような会話が分かる秀才には眠くなる内容です．
-------------------------------------------
[4] 可積分系
  http://unkar.org/r/math/1256181894
[5] シンプレクティック幾何学
  http://unkar.org/r/math/1303831839