半年以上前に、教えて!にあった作図の問題。正確には、作図の問題ではなく問題に対する質問だが。
問.与えられた3本の平行線k、l、mにそれぞれ頂点がある正三角形を作図せよ。
方法を忘れがちなので備忘録として書いておく。
直線k上に点Aをとる。
点Aから直線lに垂線を下ろし交点をBとする。

線分ABをAを中心として60°回転させ、Bの移動先をCとする。(60°は正三角形を作図する要領で描ける)

CからACの垂線を引き、直線mとの交点をDとする。

ADを結ぶ。
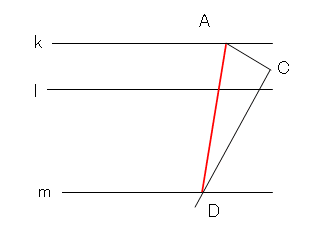
線分ADをAを中心として回転させ、直線lとの交点をEとする。

三角形ADEが求める正三角形。

| Trackback ( 0 )
|