どもども
前回取り上げた2012年東大入試理系数学第3問は回転体の体積の問題でした。
今回は応用として,極方程式で与えられた曲線を用いて作られる領域をx軸やy軸の周りに回転させて出来る立体の体積を考えてみます。

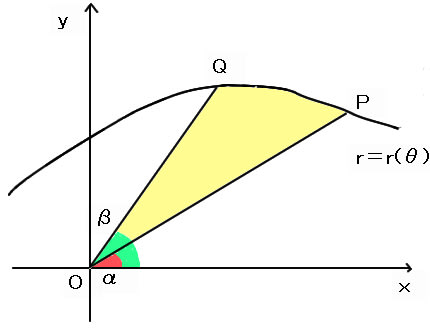
曲線C:r=r(θ)(α≦θ≦β)上の点P(r(α),α),Q(r(β),β)を取り,
線分OP,OQ,曲線Cで囲まれる領域をx軸の周りに1回転させて出来る立体の
体積を考えましょう
発想としては,曲線C上の点A(r(θ),θ),B(r(θ+Δθ),θ+Δθ)をΔθが十分小さくなるように取り,OA,OB,曲線Cで囲まれる領域をx軸周りに回転させて出来る立体の体積をΔθの2次以上の項は無視して1次近似し,それを積分により寄せ集めます。その際,下図の△OBCの回転体を考えれば十分です(残りの部分は無視できる量になります)。

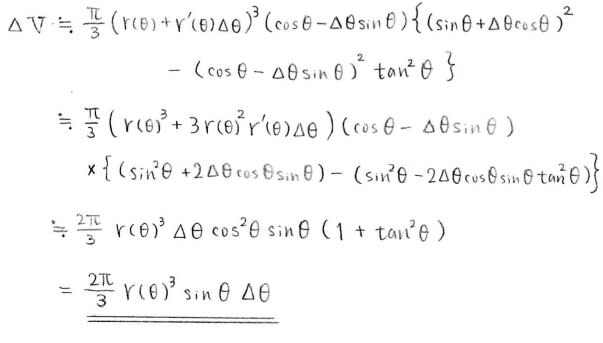

せっかくなので,前回トライした東大理系第3問で実際に使ってみます。




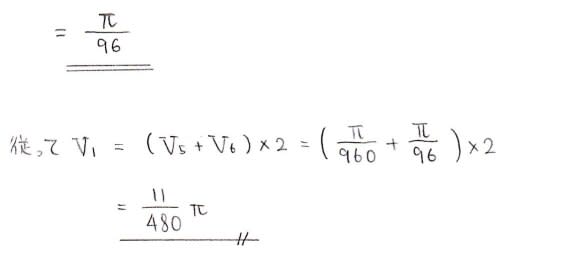
元々x,yで表された関数なので,楕円に関しては極方程式化すると面倒ですね
でも積分の上端が4/√17という嫌な数字でしかも被積分関数が無理関数だってのに,計算してみるとうまーく√17なんかが消えてくれるのはちょっと面白いです。ではV_2も同様に求めてみましょう。公式の中のsinをcosに変えるだけで実はイケます。




…とまぁ,求められるわけです。
ちなみに,楕円にはパラメータ表示(1/(√2)cosφ,1/(4√2)sinφ)があります。極座標を使うなら,これを使えばいいじゃないと思うかもしれません。
しかし,気を付けなければならないことがあります。このパラメータ表示に使われる変数φは極座標で使うθとは別物であるということです。
このφはそもそも円のパラメータ表示を元にしています。楕円というのは円を縦方向と横方向に拡大縮小したものですから,このパラメータ表示でcosφ,sinφに付いた係数はそれを反映したものになっています。

先ほど挙げた極座標を用いた回転体の体積公式を使って計算する際,φを利用しても構いませんが,それは積分の変数をθからφへと変数変換して置換積分を行っているに過ぎません。最後にこの方針で答えを求めて終わりにします。




r^3が約分されて簡単な積分に落ち着くのが面白いですね。
普通に極座標表示で計算するより幾分か簡単になったかもしれません。

前回取り上げた2012年東大入試理系数学第3問は回転体の体積の問題でした。
今回は応用として,極方程式で与えられた曲線を用いて作られる領域をx軸やy軸の周りに回転させて出来る立体の体積を考えてみます。

曲線C:r=r(θ)(α≦θ≦β)上の点P(r(α),α),Q(r(β),β)を取り,
線分OP,OQ,曲線Cで囲まれる領域をx軸の周りに1回転させて出来る立体の
体積を考えましょう

発想としては,曲線C上の点A(r(θ),θ),B(r(θ+Δθ),θ+Δθ)をΔθが十分小さくなるように取り,OA,OB,曲線Cで囲まれる領域をx軸周りに回転させて出来る立体の体積をΔθの2次以上の項は無視して1次近似し,それを積分により寄せ集めます。その際,下図の△OBCの回転体を考えれば十分です(残りの部分は無視できる量になります)。

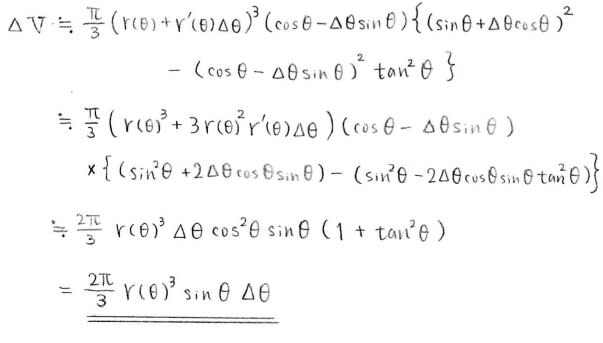

せっかくなので,前回トライした東大理系第3問で実際に使ってみます。




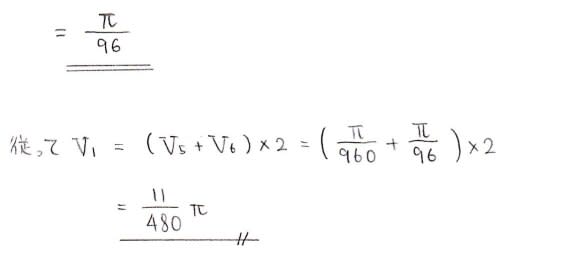
元々x,yで表された関数なので,楕円に関しては極方程式化すると面倒ですね
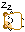
でも積分の上端が4/√17という嫌な数字でしかも被積分関数が無理関数だってのに,計算してみるとうまーく√17なんかが消えてくれるのはちょっと面白いです。ではV_2も同様に求めてみましょう。公式の中のsinをcosに変えるだけで実はイケます。




…とまぁ,求められるわけです。
ちなみに,楕円にはパラメータ表示(1/(√2)cosφ,1/(4√2)sinφ)があります。極座標を使うなら,これを使えばいいじゃないと思うかもしれません。
しかし,気を付けなければならないことがあります。このパラメータ表示に使われる変数φは極座標で使うθとは別物であるということです。
このφはそもそも円のパラメータ表示を元にしています。楕円というのは円を縦方向と横方向に拡大縮小したものですから,このパラメータ表示でcosφ,sinφに付いた係数はそれを反映したものになっています。

先ほど挙げた極座標を用いた回転体の体積公式を使って計算する際,φを利用しても構いませんが,それは積分の変数をθからφへと変数変換して置換積分を行っているに過ぎません。最後にこの方針で答えを求めて終わりにします。




r^3が約分されて簡単な積分に落ち着くのが面白いですね。
普通に極座標表示で計算するより幾分か簡単になったかもしれません。















※コメント投稿者のブログIDはブログ作成者のみに通知されます