なかなか終息しない新型コロナウイルスですが、みなさんどのような生活を送られていますか？ 私は連休明けから少しずつ少人数（クラスを分化して）で受験学年対象に教室で授業を始めました。オンライン授業も自宅からと教室からと２通りで行っております。
この間ブログへの投稿が止まり、お待たせしておりました。と言っても今回投稿する解説は、ずいぶんと荒っぽい内容になったと反省しております。前回のヒントだけよりはお役に立てるのではと思います。落ち着きましたら新しく次なるE問題を紹介したいと思います。
３番
＜解答・解説＞
答え：（1）五角形 25：72 （2 ) 台形 37：144
＜解説＞
次の３つの手順によって切り口を作図します。
① 同一平面上にある２点を直線で結ぶ。
ＱＲを直線で結びます。手順①では引けるのはこの1本だけです。
② 向かい合う面に同じ傾きの切り口の線を引く。
ＱＲに対しての向かい合う面は面ＤＨＧＣです。頂点Ｃを通るようにＱＲと同じ傾きで直線を引きます。この際面ＤＨＧＣの内部には引けないので、面を広げるようになり、手順③に移行していきます。
③ 面と線を延長し、①②にもどる。
図１のように面ＡＢＨＤと面ＥＦＧＨも広げて、 頂点Ｃを通るＱＲと同じ傾きで直線との交点をＩ，Ｋとします。面ＡＢＨＤを広げた同一面上のＩからＱを通る直線が引けます。面ＥＦＧＨを広げた面との交点をＪとします。ＪとＫは同一面上にあるので直線で結びます。すると全体が大きな三角錐となります。
傾きが同じ線により相似な三角形がたくさんできます。まず、最初に描いたＱＲにより三角形ＱＥＲは直角二等辺三角形ですから三角形ＩＤＣも三角形ＣＧＫも直角二等辺三角形とわかり、ＩＤとＧＫの長さはもとの立方体の１辺と同じ長さになります。また広げた大きな三角錐はＪＣを軸として対称形をなしています。ここで立方体の１辺の長さを１２としてそれぞれの長さを調べていきます。新たに引いた直線と立方体との交点を図１のように、Ｌ，Ｍとします。三角形ＩＬＤと三角形ＱＬＡの相似比はＩＤ：ＱＡ＝１２：６＝２：１です。よってＡＬは１２÷３×１＝４、対象の位置にあるＦＭも４になり、ＡＬ＝ＪＥ＝ＦＭ＝４です。ここからは計算です。求め方は体積比を利用する計算の工夫や直接体積を求める立式、図１、２の２通りの求積解法があります。また発想の違う解法としては、図３のように立方体の面ＡＥＦＢに手前４（ＥＪ）の高さ分直方体をくっつけると、切り口の面は新しくできた直方体の頂点ＪとＣを含む平行四辺形ＪＭＣＬとなり、この直方体を2等分していることになります。
● 三角錐をもとにする解法
ここでは図２の発想で求めてみましょう。切り口の面の上の部分が分かれた小さい方です。その体積は大きい三角錐から外にある2つの合同な三角錐を引きます。１８×１８÷２×１２÷３－６×６÷２×４÷３×２＝５０×１２です。（比で答えるために計算は最後まで行いません）また。元の立方体の体積は１２×１２×１２です。よって、５０×１２：１２×１２×１２＝２５：７２となります。
● 直方体の2等分をもとにする解法
図３の面ＡＥＦＢに手前４（ＥＪ）の高さ分の直方体から三角錐Ｊ－ＱＥＲを除いた部分を求めます。１２×１２×４－６×６÷２×４÷３＝１２×４６です。新しくできた直方体の2等分から１２×４６を除いた部部が切り口の面の上の部分になるので、１２×１２×１６÷２－１２×４６＝５０×１２です。よって、５０×１２：１２×１２×１２＝２５：７２となります。
（２）も（１）同様に考えます。
次の３つの手順によって切り口を作図します。
① 同一平面上にある２点を直線で結ぶ。
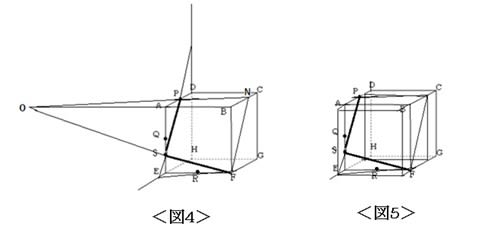
ＰＳとＳＦに直線を引きます。ＰＳと向かいある面ＢＦＧＣに頂点Ｆを通る直線を引けます。あとは手順に従い、相似形を利用して各長さを求めていきます。切り口の面によって分かれる小さい方の立体は図4のように大きい三角錐の一部になります。三角錐をもとにして求める解法と（１）のように直方体をくっつけて大きい直方体の2等分を利用する図５の解法の2通りあります。
● 三角錐をもとにする解法
ここでも立方体の１辺の長さを１２とします。図４のように三角形ＳＥＦと三角形ＳＡＯは相似形で、相似比ＳＥ：ＳＡ＝１：３よりＡＯの長さは１２×３＝３６になります。大きい三角錐と立方体の外にある三角錐の相似比は（３６+１２）：３６＝４：３より、体積比は４×４×４：３×３×３＝６４：２７となり、切り口の面によって分かれる小さい方の立体の比は６４－２７＝３７です。切り口の面によって分かれる小さい方の立体の体積は６×９÷2×３６÷３÷２７×３７＝１２×３７です。よって１２×３７：１２×１２×１２＝３７：１４４となります。
● 直方体の2等分を利用する解法
図４のＢＮの長さは相似形（三角形ＰＡＳと三角形ＮＢＦ）の利用より、１２÷3×２＝８です。図５のように立方体の面ＡＥＦＢに手前２（６÷３×１）の高さ分直方体をくっつけると、切り口の面は新しくできた直方体（面ＡＥＦＢを底面として高さが８+２＝１０）を2等分していることになります。図４の手前に出ている三角錐の体積は１２×３÷2×2÷３＝１２となり、切り口の面によって分かれる小さい方の立体の体積は１２×２×１０÷２－（１２×１２×２－１２）＝１２×３７です。よって１２×３７：１２×１２×１２＝３７：１４４となります。
４番
＜解答・解説＞
答：７９８
＜解説＞
●１周期書き出す解法
１３と１９のLCMが１周期となります。実際の数は１３×１９＝２４７となり、２４７までに書き出した整数の個数は１３+１９－１＝３１（個）です。１００÷３１＝３あまり７より３周期からあと７個書き出した数と分かります。1周期内の7番目までは書き出すと、１３、１９、２６、３８、３９、５２、５７となり、求める１００番目の数は２４７×３+５７＝７９８となります。
●歩数と歩幅の関係を利用した解法
同じ距離を進む時、歩数と歩幅は反比例の関係にあります。歩幅を１３と１９に置き換えると同じ地点まで進む歩数の比は１９：１３となります。１３から始まって目指す１００番目までに、１３+１９－１＝３１の３１個目ごとに１３と１９の公倍数に当たります。よって１００÷３１＝３あまり７よりそれぞれのべの個数の合計だと３個重複しているので１００+３＝１０３個目となります。そこまで行きつくまでのそれぞれの個数は１９：１３より、１３の倍数の個数は１０３÷（１９+１３）×１９＝６１.１・・・、１９の倍数の個数は１０３÷（１９+１３）×１３＝４１.８・・・となり、１０３個目に近いのは１９の倍数の４２番目となります。よって１９×４２＝７９８となります。
