改訂版「tanθ，cotθの一般加法定理について－その壱 2008/08/26(火)」→2022.07.21(木)

改訂版「tanθ，cotθの一般加法定理について－その壱 2008/08/26(火)」→2022.07.21(木)

[tanθ，cotθの一般加法定理について－その壱 2008_08_26(火)]

tanθの２つの角度α，βについて　 tan(α＋β)=(tanα＋tanβ)/(1-tanαtanβ）が
sinθとcosθの加法定理から出てくることはよく知られている。 それではtan(α＋β＋γ)はどうなるか？というと、
tan(α＋β＋γ)
=（tanα＋tanβ＋tanγ－tanαtanβtanγ) /(１－tanαtanβ－tanαtanγ－tanβtanγ) ・・・(*)となる。
これは、
sin(α＋β＋γ)
=sinα(cosβcosγ)＋sinβ(cosαcosγ) ＋sinγ(cosαcosβ)－sinαsinβsinγ・・(1)と

cos(α＋β＋γ)
=－cosα(sinβsinγ)－cosβ(sinαsinγ) －cosγ(sinαsinβ)＋cosαcosβcosγ・・(2)と からでる。

α＋β＋γ=180度のとき、
tan(180度)=0となるから、(*)より、次の式が成立。
tanα＋tanβ＋tanγ=tanαtanβtanγ・・・(#)

次に　cotθの定義を述べておく。

単位円周上で角θを表す同型ＯＰをとり、Ｐ(x，y)とする。このとき、cotθ=x/y　・・・(3)と 
定義するのである。
cotθは「コタンジェントθ」と読み、θの「余接」という。 定義より　

cotθ=cosθ/sinθ=1/tanθ 。
cotθの加法定理は、cot(α＋β)=(cotαcotβ－1）/(cotα＋cotβ)　・・・(4)

即ち

cot(α＋β)=－(1－cotαcotβ)/(cotα＋cotβ)・・・(5)となる。

また(2)(1)から 

cot(α＋β＋γ)
=(cotα+cotβ+cotγ－cotαcotβcotγ)/(1－cotαcotβ－cotβcotγ－cotγcotα） ・・・(**)

となる。 α＋β＋γ=180度のとき、(1)でsin(α＋β＋γ)=0となるから、 次の式が成立。

sinα(cosβcosγ)＋sinβ(cosαcosγ)＋sinγ(cosαcosβ) ＝sinαsinβsinγ
　
この両辺を sinαsinβsinγ≠0のとき、sinαsinβsinγで割れば
「cotαcotβ＋cotβcotγ＋cotγcotα=１・・・(b)」
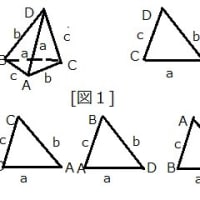
この(#)及び(b)は△ABCでも成り立つ式である。 ただし、(#)ではcosαcosβcosγ≠0
つまり、tanα，tanβ，tanγが全て定義されていなければならない。
例えば直角三角形では成立しない。 それに対してsinθは0°＜θ＜180°に対してsinθ＞0なので

cotθは、0°＜θ＜180°に対していつも定義される。0°＜θ＜90°ではcotθ＞0、
θ=90°ではcotθ=cot90°=0、。90°＜θ＜180°ではcotθ＜0となり、y=cotθは0＜θ＜180°において
単調減少で、その値は正、0、負と変化する。
そして、nを整数としてθ=180°×nが漸近線である。周期は180°である。
また
cotθ=cosθ/sinθから、cot(－θ)＝－cotθ，
cot(90°ーθ)=tanθ,よってまたtan(90°ーθ)=cotθ,さらに
cot(90°+θ)=ーtanθ,よってまたtan(90°+θ)=ーcotθとなる。

次に(2)(1)から、

cos(α＋β＋γ+δ)=cos(α＋β＋γ)cosδ－sin(α＋β＋γ)sinδ
＝－cosα(sinβsinγ)cosδ－cosβ(sinαsinγ)cosδ－cosγ(sinαsinβ)cosδ
  ＋cosαcosβcosγcosδ
  ーsinα(cosβcosγ)sinδ－sinβ(cosαcosγ)sinδ－sinγ(cosαcosβ)sinδ 
  ＋sinαsinβsinγsinδ

＝－(cosαcosδ)(sinβsinγ)－(cosβcosδ)(sinαsinγ)－(cosγcosδ)(sinαsinβ)
  ＋(cosαcosβcosγcosδ)
  －(cosαcosβ)(sinγsinδ)－(cosαcosγ)(sinβsinδ)－(cosβcosγ)(sinαsinδ)
  ＋(sinαsinβsinγsinδ)　・・・(6)

sin(α＋β＋γ+δ)
＝sin{(α＋β＋γ)+δ}=sin(α＋β＋γ)cosδ+cos(α＋β＋γ)sinδ

＝sinα(cosβcosγ)cosδ＋sinβ(cosαcosγ)cosδ＋sinγ(cosαcosβ)cosδ
　－sinαsinβsinγcosδ
－cosα(sinβsinγ)sinδ－cosβ(sinαsinγ)sinδ－cosγ(sinαsinβ)sinδ
＋cosαcosβcosγsinδ　

＝(cosβcosγcosδ)sinα＋(cosαcosγcosδ)sinβ＋(cosαcosβcosδ)sinγ　
  －cosδ(sinαsinβsinγ)
  －cosα(sinβsinγsinδ)－cosβ(sinαsinγsinδ)－cosγ(sinαsinβsinδ)　　・・・(7)
  
(6)(7)から、
cot(α＋β＋γ+δ)＝[cos(α＋β＋γ+δ)]/[sin(α＋β＋γ+δ)]
                  ＝[{－cotαcotδ－cotβcotδ－cotγcotδ＋cotαcotβcotγcotδ}
　　　　　　　　　 ＋{－cotαcotβ－cotαcotγ－cotβcotγ＋1｝]
                   /[{cotβcotγcotδ＋cotαcotγcotδ＋cotαcotβcotδ＋cotαcotβcotγ}
                     {－cotδ－cotα－cotβ－cotγ}]
                 
　　　　　　　　　＝－[1－cotαcotβ－cotαcotγ－cotαcotδ－cotβcotγ－cotβcotδ－cotγcotδ
　　　　　　　　　　　＋cotαcotβcotγcotδ]
　　　　　　　　　  /[cotα＋cotβ＋cotγ＋cotδ－cotαcotβcotγ－cotαcotβcotδ
　　　　　　　　　　 {－cotαcotγcotδ－cotβcotγcotδ}]

つまり、
cot(α＋β＋γ+δ)
＝－[1－cotαcotβ－cotαcotγ－cotαcotδ－cotβcotγ－cotβcotδ－cotγcotδ
　　　　　　　　　　　＋cotαcotβcotγcotδ]
   /[cotα＋cotβ＋cotγ＋cotδ－cotαcotβcotγ－cotαcotβcotδ－cotαcotγcotδ－cotβcotγcotδ]
　　　　　　　　　　  
　　　　・・・(8)
(5)(**)(8)から、cotθの一般加法定理の予想がつくだろう。

今回、2022.07月に、「攻撃者によって消去された」表題の［tanθ，cotθの一般加法定理について－その壱 08/08/26」
を改訂して記すにあたって、cotθのθ＝α＋β＋γ+δの場合を計算してみた。面倒なだけで本質がみえない。
私はそのような面倒なことはせずに、
[tanθの一般加法定理とn倍角の公式］の導出と同様な方法に少し手を加えただけで、苦労せずに
[cotθの一般加法定理とn倍角の公式]について簡単に導くことができた。
Wordで2001年9月8日(土)に作成している。但しB4用紙で印刷するよう保存してあるので、
pdfファイルとしてホームページ　に載せておく。