こんにちは。東久留米市の学習塾塾長です。
今回は、令和2年度灘中の問題です。
問題は、
「展開図が下の図ような立体の体積は、すべての面が1辺の長さが1cmの正三角形からなる三角すいの体積の[ ]倍です。
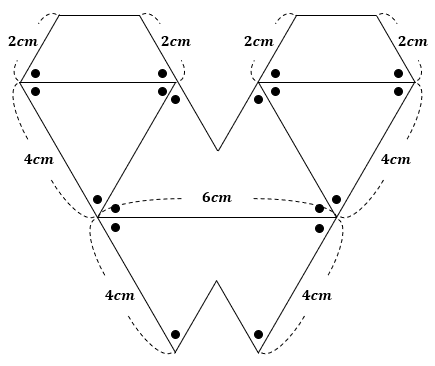
ただし、印●をつけた角の大きさはすべて60°です。」
です。
展開図の下側の面を底面にして見取り図を描くと下図のようになります。
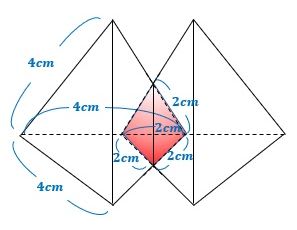
▲図.見取り図を描きました
この見取り図の左右の三角すいの体積の和から、左右の三角すいが重なっている三角すい(赤色でマークした部分)の体積を引けばOKです。
左右の三角すいは1辺4cmの正三角形からなるので、片側の体積は、1辺が1cmの三角すいの体積の
4×4×4=64(倍)
で、したがって、左右の三角すいの体積の和は、
64+64=128(倍)
になります。
一方、左右の三角すいが重なっている部分は1辺2cmの三角すいなので、その体積は、1辺が1cmの三角すいの体積の
2×2×2=8(倍)
になります。
したがって、与えられた展開図で表される立体の体積は、1辺が1cmの三角すいの体積の
128-8= 120 (倍)
で、これが答えです。
簡単な問題です。
今回は、令和2年度灘中の問題です。
問題は、
「展開図が下の図ような立体の体積は、すべての面が1辺の長さが1cmの正三角形からなる三角すいの体積の[ ]倍です。

ただし、印●をつけた角の大きさはすべて60°です。」
です。
展開図の下側の面を底面にして見取り図を描くと下図のようになります。

▲図.見取り図を描きました
この見取り図の左右の三角すいの体積の和から、左右の三角すいが重なっている三角すい(赤色でマークした部分)の体積を引けばOKです。
左右の三角すいは1辺4cmの正三角形からなるので、片側の体積は、1辺が1cmの三角すいの体積の
4×4×4=64(倍)
で、したがって、左右の三角すいの体積の和は、
64+64=128(倍)
になります。
一方、左右の三角すいが重なっている部分は1辺2cmの三角すいなので、その体積は、1辺が1cmの三角すいの体積の
2×2×2=8(倍)
になります。
したがって、与えられた展開図で表される立体の体積は、1辺が1cmの三角すいの体積の
128-8= 120 (倍)
で、これが答えです。
簡単な問題です。




















