日本数学オリンピックの簡単な問題（１０６）

こんにちは。東久留米市の学習塾塾長です。

朝は晴れてぽかぽか陽気だったのですが、昼過ぎから雲が出て気温は頭打ちになり、夕方前から下がり始めるようです。明日は平年並みの気温ですが、それ以降は少し寒い日が続くようです。風邪などひかぬよう暖かくして過ごしましょう。

さて、今回は２０１７年日本数学オリンピック予選に出題された場合の数の問題を取り上げます。

問題は、
「ａ＋ｂ＝ｃ＋ｄ＋ｅ＝２９ となる、相異なる正の整数の組（ａ，ｂ，ｃ，ｄ，ｅ）はいくつあるか。」
です。

早速、取り掛かりましょう。

等式が２つありますが、ここは、ｃ＋ｄ＋ｅ＝２９ を先に調べましょう。

この等式を満たす正の整数ｃ、ｄ、ｅは、例えば、２９個の球を並べ、２８ヶ所ある球と球の間に２つの仕切りを入れ、３つのグループに分けられた球の個数をそれぞれｃ、ｄ、ｅに割り振れば、ｃ、ｄ、ｅを決めることができます。

つまり、ｃ、ｄ、ｅの組合せの個数は２８ヶ所から仕切りを入れる２ヶ所の選び方になり、それは、
28Ｃ2＝２８×２７/（２×１）＝３７８通り
です。

ところが、問題の条件にａ、ｂ、ｃ、ｄ、ｅは相異なる正の整数とあるので、上で計算した３７８通りから、ｃ、ｄ、ｅのいずれかが等しくなる場合の数を差し引かなければなりません。

そこで、２つ以上が等しい３つの正の整数で、それらの和が２９になるものの組合せを調べると、
（１，１，２７）、 （２，２，２５）、（３，３，２３）、（４，４，２１）、（５，５，１９）、
（６，６，１７）、（７，７，１５）、（８，８，１３）、（９，９，１１）、（１０，１０，９）、
（１１，１１，７）、（１２，１２，５）、（１３，１３，３）、（１４，１４，１）
の１４通りあることが判ります。

そして、これらの３つの整数のｃ、ｄ、ｅへの割り振り方は３通りなので、ｃ、ｄ、ｅのいずれかが等しくなる場合の数は、
１４×３＝４２通り
になります。

したがって、ｃ＋ｄ＋ｅ＝２９を満たす相異なる正の整数の組（ｃ，ｄ，ｅ）は、
３７８－４２＝３３６通り
になります。

続いて、ａ＋ｂ＝２９です。

この等式を満たす正の整数ａ、ｂの組合せの個数は、上と同じように、並べた球の間に仕切りを入れることを考えれば勘定できます。

このときａ＋ｂ＝２９なので、ａとｂは等しくならないのですが、ａまたはｂがｃ、ｄ、ｅと等しくなる場合の数を差し引かなければなりません。

そこで下図のように、あるｃ、ｄ、ｅの組合せについて、ｃ、ｄ、ｅの順番を入れ替えたときの仕切りの位置を調べます。

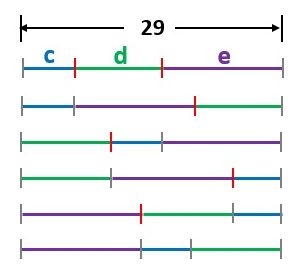
▲図．あるｃ、ｄ、ｅについて、それらの順番を入れ替えたときの仕切りの位置です

この図の赤色線でマークした６ヶ所の仕切りに、ａ、ｂを分ける仕切りを入れた場合、ａまたはｂがｃ、ｄ、ｅのいずれかと等しくなってしまうことが判ります。

つまり、ａ、ｂの仕切りは、あるｃ、ｄ、ｅの組合せに対して、２８－６＝２２ヶ所の球と球の間にいれなければなりません。

したがって、ａ＋ｂ＝２９を満たし、ａ、ｂ、ｃ、ｄ、ｅが相異なる正の整数の組（ａ，ｂ）は、
22Ｃ1＝２２通り
になります。

以上から、ａ＋ｂ＝ｃ＋ｄ＋ｅ＝２９となる、相異なる正の整数の組（ａ，ｂ，ｃ，ｄ，ｅ）は、
３３６×２２＝７３９２通り
で、これが答えです。


５つの整数が相異なるということを失念しなければ簡単な問題です。