こんにちは。東久留米市の学習塾塾長です。
昨日と同じように、暖かく穏やかな天気になりました。明日も暖かくなるようですが、明後日から冷え込むようです。風邪などひかぬよう暖かくして過ごしましょう。
さて、今回は2003年日本数学オリンピック本選に出題された図形問題を取り上げます。
問題は、
「三角形ABCの内部に点Pをとり、直線BPと辺ACの交点をQ、直線CPと辺ABの交点をRとする。
AR=RB=CP かつ CQ=PQ
であるとき、∠BRCの大きさを求めよ。
ただし、2点X、Yに対し、線分XYの長さをXYで表している。」
です。
早速、図1のように、問題の図を描きましょう。
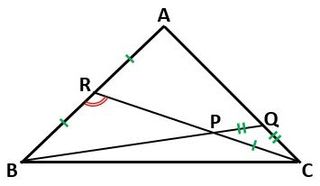
▲図1.問題の図を描きました
ここは、△ABQと線分CRについて、メネラウスの定理を使うのがよいでしょう。
すると、
RB/AR・PQ/BP・CA/QC=1 (1)
が成り立ちます。
このとき、
AR=RB=CP かつ CQ=PQ
ですから、(1)は、
RB/RB・PQ/BP・CA/PQ=CA/BP=1
になり、したがって、図2に示すように、
CA=BP
になります。

▲図2.CA=BPです
また、図3に示すように、△QCPが二等辺三角形なので、
∠QCP=∠QPC
です。
さらに、対頂角は等しいので、
∠QPC=∠BPR
で、したがって、
∠QCP=∠BPR
になります。

▲図3.∠QCP=∠BPRです
すると、辺CAと辺PB、∠QCPと∠BPRをもつ合同な三角形を作りたくなります。
そこで、図4のように、線分CR上に、RS=RBになる点Sをとり、△CASと△BPRを作りましょう。
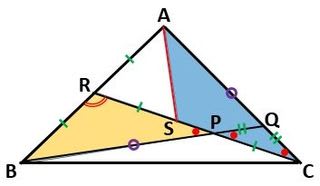
▲図4.線分CR上に、RS=RBになる点Sをとり、△CASと△BPRを作りました
すると、
CS=CP+PS
=RS+PS
=PR
になり、
△CAS≡△BPR (2組の辺とその間の角が等しい)
です。
そして、合同な三角形の対応する辺の長さは等しいので、
AS=RB (2)
であることが判ります。
一方、仮定より、
AR=RB
で、これと(2)から
AR=RB=AS
になり、△ARSは正三角形になります。
したがって、
∠BRC=180°-∠ARC
=180°-∠ARS
=180°-60°
=120°
で、これが答えです。
見通しのよい問題です。
昨日と同じように、暖かく穏やかな天気になりました。明日も暖かくなるようですが、明後日から冷え込むようです。風邪などひかぬよう暖かくして過ごしましょう。
さて、今回は2003年日本数学オリンピック本選に出題された図形問題を取り上げます。
問題は、
「三角形ABCの内部に点Pをとり、直線BPと辺ACの交点をQ、直線CPと辺ABの交点をRとする。
AR=RB=CP かつ CQ=PQ
であるとき、∠BRCの大きさを求めよ。
ただし、2点X、Yに対し、線分XYの長さをXYで表している。」
です。
早速、図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
ここは、△ABQと線分CRについて、メネラウスの定理を使うのがよいでしょう。
すると、
RB/AR・PQ/BP・CA/QC=1 (1)
が成り立ちます。
このとき、
AR=RB=CP かつ CQ=PQ
ですから、(1)は、
RB/RB・PQ/BP・CA/PQ=CA/BP=1
になり、したがって、図2に示すように、
CA=BP
になります。

▲図2.CA=BPです
また、図3に示すように、△QCPが二等辺三角形なので、
∠QCP=∠QPC
です。
さらに、対頂角は等しいので、
∠QPC=∠BPR
で、したがって、
∠QCP=∠BPR
になります。

▲図3.∠QCP=∠BPRです
すると、辺CAと辺PB、∠QCPと∠BPRをもつ合同な三角形を作りたくなります。
そこで、図4のように、線分CR上に、RS=RBになる点Sをとり、△CASと△BPRを作りましょう。

▲図4.線分CR上に、RS=RBになる点Sをとり、△CASと△BPRを作りました
すると、
CS=CP+PS
=RS+PS
=PR
になり、
△CAS≡△BPR (2組の辺とその間の角が等しい)
です。
そして、合同な三角形の対応する辺の長さは等しいので、
AS=RB (2)
であることが判ります。
一方、仮定より、
AR=RB
で、これと(2)から
AR=RB=AS
になり、△ARSは正三角形になります。
したがって、
∠BRC=180°-∠ARC
=180°-∠ARS
=180°-60°
=120°
で、これが答えです。
見通しのよい問題です。




















