こんにちは。東久留米市の学習塾塾長です。
今回は、2019年日本ジュニア数学オリンピック本選に出題された整数問題を取り上げます。
問題は、
「a、bを正の整数とする。
(1)不等式

が成立することを示せ。
(2)この不等式の等号が成立するような正の整数の組(a,b)をすべて求めよ。
ただし、正の整数x、yに対し、xとyの最大公約数をgcd(x,y)で表し、xとyのうち小さい数をmin(x,y)で表す。なお、x=yのときはmin(x,y)=xとする。」
です。
早速、取り掛かりましょう。
gcd(a,b+1)、gcd(a+1,b)のままでは扱い難いので、それぞれをMとNとしましょう。
すると、a、b+1 はMの倍数で、a+1、bはNの倍数なので、
a =kM 〔1〕
b+1=lM 〔2〕
a+1=sN 〔3〕
b =tN 〔4〕
と表すことができます。このとき、k、l、s、tは正の整数です。
また、与えられた不等式は、aとbを交換しても同じ不等式になるので、M≦Nとして進めます。
〔1〕と〔4〕、〔2〕と〔3〕の辺々を掛け合わせると、それぞれ、
ab=ktMN 〔5〕
(a+1)(b+1)=lsMN 〔6〕
になります。
さらに、〔5〕と〔6〕の辺々の差をとると、
(a+1)(b+1)-ab=ab+a+b+1-ab
=a+b+1
=lsMN-ktMN
=(ls-kt)MN
で、これから
a+b+1=(ls-kt)MN
なので、a+b+1はMNの倍数になります。
したがって、
a+b+1≧MN 〔7〕
です。
ここから、M=Nと、M<N、つまりM+1≦Nに場合分けして調べます。
● M=Nの場合
〔1〕と〔3〕から
a =kM
a+1=sM
になり、このとき、aとa+1は互いに素なので、M=1になります。
すると、与えられた不等式の左辺は1になり、一方、
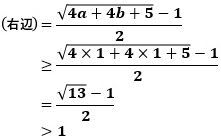
なので、与えられた不等式は、等号を除いて、成り立ちます。
● M<N⇒M+1≦Nの場合
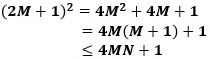
で、このとき〔7〕から
4MN+1≦4(a+b+1)+1
=4a+4b+5
が成り立ちます。(不等式右辺の根号内の式が現れました)
これを整理すると、
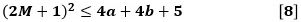
になります。
あとは〔8〕を使って、与えられた不等式の右辺を変形するだけです。
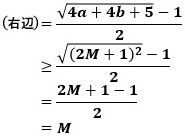
で、左辺はMなので、与えられた不等式は成り立ちます。このとき、等号が成立するのは、N=M+1、MN=a+b+1のときです。
以上から、与えられた不等式が成り立つことを示すことができました。
(2)は次回に取り上げます。
今回は、2019年日本ジュニア数学オリンピック本選に出題された整数問題を取り上げます。
問題は、
「a、bを正の整数とする。
(1)不等式

が成立することを示せ。
(2)この不等式の等号が成立するような正の整数の組(a,b)をすべて求めよ。
ただし、正の整数x、yに対し、xとyの最大公約数をgcd(x,y)で表し、xとyのうち小さい数をmin(x,y)で表す。なお、x=yのときはmin(x,y)=xとする。」
です。
早速、取り掛かりましょう。
gcd(a,b+1)、gcd(a+1,b)のままでは扱い難いので、それぞれをMとNとしましょう。
すると、a、b+1 はMの倍数で、a+1、bはNの倍数なので、
a =kM 〔1〕
b+1=lM 〔2〕
a+1=sN 〔3〕
b =tN 〔4〕
と表すことができます。このとき、k、l、s、tは正の整数です。
また、与えられた不等式は、aとbを交換しても同じ不等式になるので、M≦Nとして進めます。
〔1〕と〔4〕、〔2〕と〔3〕の辺々を掛け合わせると、それぞれ、
ab=ktMN 〔5〕
(a+1)(b+1)=lsMN 〔6〕
になります。
さらに、〔5〕と〔6〕の辺々の差をとると、
(a+1)(b+1)-ab=ab+a+b+1-ab
=a+b+1
=lsMN-ktMN
=(ls-kt)MN
で、これから
a+b+1=(ls-kt)MN
なので、a+b+1はMNの倍数になります。
したがって、
a+b+1≧MN 〔7〕
です。
ここから、M=Nと、M<N、つまりM+1≦Nに場合分けして調べます。
● M=Nの場合
〔1〕と〔3〕から
a =kM
a+1=sM
になり、このとき、aとa+1は互いに素なので、M=1になります。
すると、与えられた不等式の左辺は1になり、一方、
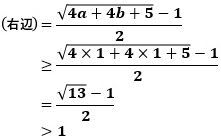
なので、与えられた不等式は、等号を除いて、成り立ちます。
● M<N⇒M+1≦Nの場合
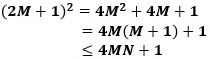
で、このとき〔7〕から
4MN+1≦4(a+b+1)+1
=4a+4b+5
が成り立ちます。(不等式右辺の根号内の式が現れました)
これを整理すると、
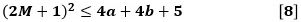
になります。
あとは〔8〕を使って、与えられた不等式の右辺を変形するだけです。
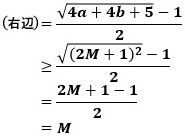
で、左辺はMなので、与えられた不等式は成り立ちます。このとき、等号が成立するのは、N=M+1、MN=a+b+1のときです。
以上から、与えられた不等式が成り立つことを示すことができました。
(2)は次回に取り上げます。










