こんにちは。東久留米市の学習塾塾長です。
今回は、平成31年度東大入試問題(前期、理系)です。
問題は、
「nを1以上の整数とする。
(1)

の最大公約数dn を求めよ。
(2)

が整数の2乗にならないことを示せ。」
です。
早速、取り掛かりましょう。
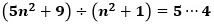
なので、ユークリッドの互除法から、与えられた2つの式の最大公約数dn は、
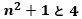
の最大公約数になります。
ここで、nが偶数の場合と奇数の場合に分けて調べましょう。
● nが偶数の場合
n=2k (kは1以上の整数)とすると、

で、このとき、

は整数なので、

は奇数になります。
一方、4の約数は 1、2、4なので、
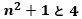
の最大公約数は1になります。
したがって、nが偶数のとき、dnは1です。
● nが奇数の場合
n=2k+1 (kは0以上の整数)とすると、

で、このとき

は奇数なので、

は2の倍数、かつ、4の倍数ではありません。
したがって、nが奇数のとき、dnは2です。
まとめると、
nが偶数のとき、dn=1
nが奇数のとき、dn=2
で、これが答えです。
続いて(2)です。
(1)を利用するため、nが偶数の場合と奇数の場合に分けて調べましょう。
● nが偶数の場合

の最大公約数は1なので、これらの2式の積が整数の2乗になるためには、いずれの式も整数も整数の2乗にならなくてはなりません。
ところが、

から

は整数の2乗ではありません。
したがって、

は整数の2乗ではありません。
● nが奇数の場合
(1)から

の最大公約数は2なので、
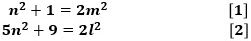
(mとlは1以上の互いに素な整数)
とおくことができます。
ここで、〔2〕-〔1〕から

です。
このとき、

が奇数から
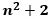
は奇数なので、左辺は2の倍数で4の倍数ではありません。
一方、l-mとl+mの偶奇は同じなので、右辺は奇数または4の倍数になり、〔3〕は成り立ちません。
したがって、

は整数の2乗ではありません。
以上から、

は整数の2乗にならないことを示すことができました。
簡単な問題です。
今回は、平成31年度東大入試問題(前期、理系)です。
問題は、
「nを1以上の整数とする。
(1)

の最大公約数dn を求めよ。
(2)

が整数の2乗にならないことを示せ。」
です。
早速、取り掛かりましょう。
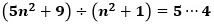
なので、ユークリッドの互除法から、与えられた2つの式の最大公約数dn は、
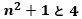
の最大公約数になります。
ここで、nが偶数の場合と奇数の場合に分けて調べましょう。
● nが偶数の場合
n=2k (kは1以上の整数)とすると、

で、このとき、

は整数なので、

は奇数になります。
一方、4の約数は 1、2、4なので、
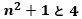
の最大公約数は1になります。
したがって、nが偶数のとき、dnは1です。
● nが奇数の場合
n=2k+1 (kは0以上の整数)とすると、

で、このとき

は奇数なので、

は2の倍数、かつ、4の倍数ではありません。
したがって、nが奇数のとき、dnは2です。
まとめると、
nが偶数のとき、dn=1
nが奇数のとき、dn=2
で、これが答えです。
続いて(2)です。
(1)を利用するため、nが偶数の場合と奇数の場合に分けて調べましょう。
● nが偶数の場合

の最大公約数は1なので、これらの2式の積が整数の2乗になるためには、いずれの式も整数も整数の2乗にならなくてはなりません。
ところが、

から

は整数の2乗ではありません。
したがって、

は整数の2乗ではありません。
● nが奇数の場合
(1)から

の最大公約数は2なので、
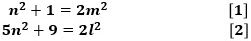
(mとlは1以上の互いに素な整数)
とおくことができます。
ここで、〔2〕-〔1〕から

です。
このとき、

が奇数から
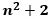
は奇数なので、左辺は2の倍数で4の倍数ではありません。
一方、l-mとl+mの偶奇は同じなので、右辺は奇数または4の倍数になり、〔3〕は成り立ちません。
したがって、

は整数の2乗ではありません。
以上から、

は整数の2乗にならないことを示すことができました。
簡単な問題です。










