速さの比較、離心円と楕円

プトレマイオスの離心円上の惑星とケプラーの楕円上の惑星の速さを比較してみよう。

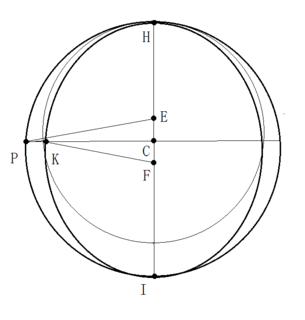
楕円軌道上の惑星は、面積法則（面積一定の速度）で回転する。遠日点Hでの速さをv₀、遠日点から90°の点Kでの速さをv_K、近日点Iでの速さをv_xとする。Fからの距離に着目すると、
FH ＝1＋e
FI ＝1－e
FK ＝1
である。だから、面積法則より、次の関係が成り立つ。
1/2･(1＋e)･v₀＝1/2･(1－e)･v_x＝1/2･1･v_K
したがって（前2項より）、v_x＝(1＋e)/(1－e)･v₀
また（両端より）、v_K＝(1＋e)･v₀
である。
他方、離心円上の惑星は、等化点（エカント）Eのまわりを一定の角速度ωで回転する。遠日点Hでの速さをv₀、遠日点から90°の点Pでの速さをv_P、近日点Iでの速さをv_yとする。Eからの距離に着目すると、
EH ＝1－e
EI ＝1＋e
EK ＝√(1＋e²)
である。だから、次の関係が成り立っている。
v₀＝(1－e)ω　　　(1)
v_y＝(1＋e)ω　　　(2)
v_P＝√(1＋e²)ω　　(3)
(1)より、
ω＝v₀/(1－e)　　　(∗)
(2)に入れて、
v_y＝(1＋e)/(1－e)･v₀
したがって、v_x＝v_yとなり、近日点では同じ速さで回転していることがわかる。
(∗)を(3)に入れると、
v_P＝√(1＋e²)/(1－e)･v₀
ここで、1/(1－e)＝1＋e＋e²＋…
また、√(1＋e²)＝1＋1/2･e²－1/8･e⁴＋…
だから、
v_P＝(1＋1/2･e²－1/8･e⁴＋…)(1＋e＋e²＋…)
となる。ここで、離心率eの1次までとると、
v_P≒(1＋e)･v₀
したがって、v_P≒v_K
遠日点から90°の地点ではほぼ同じ速さで回転していることがわかる。

プトレマイオスの離心円上の惑星とケプラーの楕円上の惑星はほぼ同じ速さで回転している。プトレマイオスのモデルはケプラーの第１法則（楕円）と第２法則（面積）のとても良い近似だったのである。

参考文献
「プトレマイオス天動説のエカントとコペルニクス地動説の周転円」（「FNの高校物理」）