こんにちは。東久留米市の学習塾塾長です。
昨夜からしっかりとした雨が降っています。東久留米の気温は20℃で、涼しいを通り越して少し寒いほどです。明日は暖かくなるようですが、風邪など引かぬよう気をつけましょう。
さて、今回は2005年日本数学オリンピック予選に出題された図形問題を取り上げます。
問題は、
「OA=2、OP=a、∠AOP=90°なる直角三角形AOPの辺OAの中点を点Bとする。このとき∠APBを最大にするようなaの値を求めよ。」
です。
以前に取り上げた京大入試問題に同じようなものがあります。(中学生でも手が届く京大入試問題(12))
初めに、図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
次に、図2のように、AとBを通り、直線OPに接する円Cを描きます。

▲図2.AとBを通り、直線OPに接する円Cを描きました
ここで、円Cと直線OPとの接点をP’とすると、P’を除く直線OP上のすべての点Pは、円Cの外部にあるので、∠AP’B>∠APBになり、PがP’に一致するとき、∠APBは最大になります。
そこで、図3のように、Pを接点とした図に描き直しましょう。

▲図3.Pを接点にしました
図3で、Cから辺OAに垂線を下ろし、その足をDとします。
このとき、△CABは二等辺三角形なので、Dは線分ABの中点で、AD=BD=1/2、さらに、OD=1+1/2=3/2です。
一方、DO=CPで、CPは円Cの半径なので、CP=CAが成り立ち、したがって、CA=3/2になります。
そこで、直角三角形CADに三平方の定理を適用して、
CA^2=AD^2+CD^2
(3/2)^2=(1/2)^2+CD^2
CD^2=9/4-1/4
=2
から
CD=√2
です。
ここで、CD=OP=aですから、∠APBが最大になるのは
a=√2
のときで、これが答えです。
続いて、高校で勉強する三角関数を使って解いてみましょう。
図5のように、∠APB=θとします。

▲図5.三角関数を利用します
図5で、辺APと線分BPの長さは、三平方の定理から、それぞれ、√(a^2+4)および√(a^2+1)です。
ここで、△PABに余弦定理を適用すると、

が成り立ちます。
このとき、0°<θ<90° (θ=90°になるのは、Pが線分ABを直径とする円の周上にあるときで、この円は図5の直線OPと交わりません)なので、θが最大になるのは、cosθが最小になるときです。
つまり、上式の根号のなかにある、a^2+5+4/a^2 が最小のとき、cosθが最小になり、θが最大になります。
そこで、相加相乗平均の不等式から
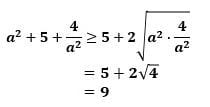
が成立し、ここで等号は、
a^2=2
のとき成り立ちます。
したがって、a=√2のとき、θは最大になります。
前半の解き方のA、Bを通り、直線OPに接する円を描くテクニックを頭に入れておくと役に立つことがあるかも知れません。
昨夜からしっかりとした雨が降っています。東久留米の気温は20℃で、涼しいを通り越して少し寒いほどです。明日は暖かくなるようですが、風邪など引かぬよう気をつけましょう。
さて、今回は2005年日本数学オリンピック予選に出題された図形問題を取り上げます。
問題は、
「OA=2、OP=a、∠AOP=90°なる直角三角形AOPの辺OAの中点を点Bとする。このとき∠APBを最大にするようなaの値を求めよ。」
です。
以前に取り上げた京大入試問題に同じようなものがあります。(中学生でも手が届く京大入試問題(12))
初めに、図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
次に、図2のように、AとBを通り、直線OPに接する円Cを描きます。

▲図2.AとBを通り、直線OPに接する円Cを描きました
ここで、円Cと直線OPとの接点をP’とすると、P’を除く直線OP上のすべての点Pは、円Cの外部にあるので、∠AP’B>∠APBになり、PがP’に一致するとき、∠APBは最大になります。
そこで、図3のように、Pを接点とした図に描き直しましょう。

▲図3.Pを接点にしました
図3で、Cから辺OAに垂線を下ろし、その足をDとします。
このとき、△CABは二等辺三角形なので、Dは線分ABの中点で、AD=BD=1/2、さらに、OD=1+1/2=3/2です。
一方、DO=CPで、CPは円Cの半径なので、CP=CAが成り立ち、したがって、CA=3/2になります。
そこで、直角三角形CADに三平方の定理を適用して、
CA^2=AD^2+CD^2
(3/2)^2=(1/2)^2+CD^2
CD^2=9/4-1/4
=2
から
CD=√2
です。
ここで、CD=OP=aですから、∠APBが最大になるのは
a=√2
のときで、これが答えです。
続いて、高校で勉強する三角関数を使って解いてみましょう。
図5のように、∠APB=θとします。

▲図5.三角関数を利用します
図5で、辺APと線分BPの長さは、三平方の定理から、それぞれ、√(a^2+4)および√(a^2+1)です。
ここで、△PABに余弦定理を適用すると、

が成り立ちます。
このとき、0°<θ<90° (θ=90°になるのは、Pが線分ABを直径とする円の周上にあるときで、この円は図5の直線OPと交わりません)なので、θが最大になるのは、cosθが最小になるときです。
つまり、上式の根号のなかにある、a^2+5+4/a^2 が最小のとき、cosθが最小になり、θが最大になります。
そこで、相加相乗平均の不等式から
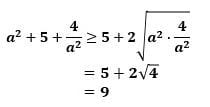
が成立し、ここで等号は、
a^2=2
のとき成り立ちます。
したがって、a=√2のとき、θは最大になります。
前半の解き方のA、Bを通り、直線OPに接する円を描くテクニックを頭に入れておくと役に立つことがあるかも知れません。




















